¿Cómo medir el cambio de área bajo la curva

Puede utilizar una función de área para medir el área bajo una curva, así como la zona cambios. Por ejemplo, digamos que usted tiene cualquier función de edad, F (t). Imagínese que en algún t-valor, lo llaman s, se dibuja una línea vertical fijo, como se muestra.

Luego de tomar una línea vertical móvil, comenzando en el mismo punto, s ("s" es para comenzando punto), y arrastre hacia la derecha. A medida que arrastra la línea, usted barre un área más grande y más grande bajo la curva. Esta zona es una función de X, la posición de la línea móvil. En símbolos, escribes

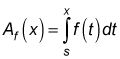
Tenga en cuenta que t es la variable de entrada en F (t) en lugar de X porque X ya está tomada - es la variable de entrada en LA_F (X). El subíndice F en LA_F indica que LA_F (X) Es la función de área para la curva en particular F o F (t). los dt es un pequeño incremento a lo largo del t-eje - en realidad una infinitesimalmente pequeño incremento.

He aquí un ejemplo sencillo para asegurarse de que usted tiene una manija en cómo funciona una función de área. Por cierto, no te sientas mal si usted encuentra este muy difícil de entender - que tienes mucha compañía. Digamos que tienes la función simple, F (t) = 10, que es una línea horizontal en y = 10. Si barrer el área a partir de las s = 3, se obtiene la siguiente función de zona:

Usted puede ver que el área barrida 3-4 es 10 porque, arrastrando la línea de 3 a 4, se barre un rectángulo con un ancho de 1 y una altura de 10, que tiene una superficie de 1 Tiempos 10, o 10, como se muestra aquí.

Por lo tanto, LA_F (4), el área de barrido como se golpeó 4, es igual a 10. LA_F (5) es igual a 20, porque cuando se arrastra la línea de 5, que ha arrastrado un rectángulo con un ancho de 2 y altura de 10, que tiene una superficie de 2 veces 10 o 20. LA_F (6) es igual a 30, y así sucesivamente.

Ahora, imagina que arrastra la línea a lo largo a razón de una unidad por segundo. Usted comienza en X = 3, y se golpea 4 a 1 segundo, 5 segundos a los 2, 6 a los 3 segundos, y así sucesivamente. ¿Cuánta área está barriendo a cabo por segundo? Diez unidades cuadrados por segundo debido a que cada segundo que barrer otro rectángulo de 1 por 10. Aviso - esto es enorme - que, debido a la anchura de cada rectángulo que barren es 1, el área de cada rectángulo - que está dada por altura veces ancho - es el mismo que su altura porque los tiempos cualquier cosa 1 es igual a sí mismo. Ves por qué esto es muy importante en un minuto. (Por cierto, la tasa real que te importa aquí no es el área barrida por segundo, sino, más bien, área barrida por unidad de cambio en el X-eje. En este ejemplo se explica en términos de por segundo porque es más fácil pensar en una tasa de barrido de salida del área de esta manera. Y ya que está arrastrando la línea a través de uno x-unidad de eje por uno segundo, ambas tasas son las mismas. Elige tu opción.)

La derivada de una función de área igual a la tasa de área que está siendo barrida. Bueno, estás sentado? Has alcanzado otro de los grandes Ah, ja! momentos en la historia de las matemáticas. Recordemos que Un derivado es una tasa. Por lo tanto, debido a que la velocidad a la que la función de área anterior crece es de 10 unidades cuadradas por segundo, se puede decir su derivada es igual a 10. Por lo tanto, se puede escribir

De nuevo, esto sólo te dice que con cada aumento de 1 unidad en X, LA_F (la función de área) sube 10. Ahora aquí es la cosa fundamental: Tenga en cuenta que esta tasa o derivado de la 10 es la misma que la altura de la función original F (t) = 10, porque a medida que avanza a través de 1 unidad, usted barre un rectángulo que es 1 por 10, que tiene una superficie de 10, la altura de la función.

Y la tasa funciona a 10 independientemente de la anchura del rectángulo. Imagina que arrastra la línea vertical desde X = 4 a X = 4.001. A razón de una unidad por segundo, que le llevará 1/1000^º segundo, y se le barre un rectángulo delgado, con una anchura de 1/1000, una altura de 10, y por lo tanto un área de 10 veces 1/1000, o 1/100 unidades cuadradas. La tasa de área que está siendo barrida sería, por lo tanto,

lo que equivale a 10 unidades cuadrados por segundo. Así que ya ves que con cada pequeño incremento a lo largo del X-eje, la tasa de área que está siendo barrido es igual a la altura de la función.

Esto funciona para cualquier función, no sólo de las líneas horizontales. Mira la función g (t) Y su función de área LA_g (X) Que barre la zona a partir de las s = 2 en la siguiente figura.

Entre X = 3,6 y X = 3,7, LA_g (X) Crece por el área de ese flaco, oscura sombra "rectángulo" con una anchura de 0,1 y una altura de aproximadamente 15. (Como se puede ver, no es realmente un rectangle- está más cerca de un trapecio, pero no es que sea porque su diminuto superior se curva ligeramente. Pero, en el límite, como la anchura se hace más pequeño y más pequeño, el "rectángulo" flaco se comporta exactamente como un verdadero rectángulo.) Así que, para repetir, LA_g (X) Crece por el área de ese oscuro "rectángulo", que tiene una superficie extremadamente cerca de 0,1 veces 15, o 1.5. Esa área es barrido en 0,1 segundos, por lo que el índice de área que está siendo barrido es

o 15 unidades cuadrados por segundo, la altura de la función. Esta idea es tan importante que merece ser repetido:

La tasa de área de barrer es igual a la altura. los tarifa del área que está siendo barrido bajo una curva mediante una función de área en un determinado X-valor es igual a la altura de la curva en ese X-valor.