Cómo aproximar el área del punto medio con rectángulos
Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la izquierda; rectángulo o derecho; rectángulo suma. La siguiente figura muestra por qué.
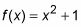
Se puede ver en la figura que la parte de cada rectángulo que está por encima de la curva se ve sobre el mismo tamaño que la brecha entre el rectángulo y la curva. Una suma punto medio produce una buena estimación tales porque estos dos errores más o menos se anulan entre sí.
La figura anterior muestra la forma en que tendría que utilizar tres rectángulos punto medio para estimar el área bajo
de 0 a 3. Para los tres rectángulos, sus anchuras son 1 y sus alturas son F(0,5) = 1,25, F(1,5) = 3,25, y F(2,5) = 7,25. Area = base X altura, por lo que añadir 1,25 + 3,25 + 7,25 para obtener el área total de 11.75.
El uso de la integral definida, se encuentra que el área exacta bajo esta curva resulta ser 12, por lo que el error en esta estimación de tres punto medio-rectángulos es 0,25. Esto contrasta con el mucho peores errores de los tres-izquierda; rectángulos estiman y los tres de derecha; rectángulos estimación de 4,0 y 5,0, respectivamente.
Aquí está la regla del punto medio oficial:
Punto medio Regla del rectángulo-Usted puede aproximar el área exacta bajo una curva entre la y b,
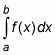
con una suma de rectángulos punto medio dado por la siguiente fórmula. En general, cuanto más rectángulos, mejor será la estimación:
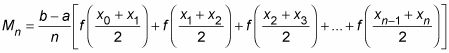
Dónde, n es el número de rectángulos,
es el ancho de cada rectángulo, y los valores de la función son las alturas de los rectángulos.
-
Cómo dibujar transparente en JavaFX -
Encuentre el área de polígonos en matemáticas núcleo común -
Cómo determinar el área de rectángulos compuestos -
10 Cosas para recordar acerca de la integración y cálculo -
Encuentra las zonas exactas bajo una curva mediante la integral definida -
¿Cómo funciona la integración: es sólo Además de lujo
Cómo estadísticas muestra la conexión entre la diferenciación y la integración Aún tratando de entender cómo el trabajo de diferenciación e integración? No hay problema: se puede usar las estadísticas para ayudarle. Mediante el estudio de la relación entre dos gráficos simples, vas a entender la relación entre la…
Cómo aproximar área con la regla de Simpson Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo hacer una aproximación área usando la notación sigma Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
¿Cómo encontrar el valor medio con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…
Cómo utilizar la notación sigma para encontrar el área bajo una curva Puede usar la notación sigma para escribir la suma de Riemann para una curva. Esto es útil cuando se quiere derivar la fórmula para el área aproximada bajo la curva. Por ejemplo, digamos que usted desea encontrar el área aproximada de n…
Cómo escribir sumas de Riemann con la notación sigma Puede usar la notación sigma para escribir la derecha; suma rectángulo para una función. Por ejemplo, digamos que tienes F (X) = X2 + 1.Por cierto, no es necesario la notación sigma para la matemáticas que sigue. Es sólo una " conveniencia " -…
La definición de la integral definida y cómo funciona Usted puede aproximar el área bajo una curva mediante la suma de la derecha, izquierda o rectángulos punto medio. Para encontrar un área exacta, es necesario utilizar una integral definida.Al aproximar el área bajo una curva, la parte superior…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Cómo calcular el área de un trapecio Usted puede utilizar el derecho; truco triángulo para encontrar el área de un trapecio. La siguiente trapezoide TRAP parece un trapecio isósceles, ¿no? No se olvide - las apariencias engañan.Usted debe estar pensando, triángulos rectángulos,…