Cómo aproximar área con la regla de Simpson
Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson como los verdaderos trapezoides juegan en la regla trapezoidal. Echa un vistazo a tres de estas formas curvilíneas-coronado en la siguiente figura.
En contraste con la manera intervalos se utilizan en la izquierda ;, derecho; y las reglas de punto medio-rectángulo y en la regla trapezoidal, necesita dos intervalos (en lugar de uno) para cada " trapezoide " en la regla de Simpson.
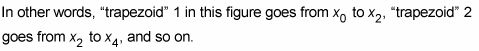
Debido a esto, la duración total de siempre debe estar dividida en un número par de intervalos.
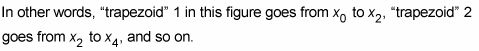
La regla de Simpson es un método de aproximación muy precisa. De hecho, se da el área exacta para cualquier función polinomio de grado tres o menos. En general, la regla de Simpson da una estimación mucho mejor que cualquiera de la regla del punto medio o la regla trapezoidal.
Una de Simpson suma regla o aproximación es una especie de un promedio de una suma punto medio y una suma trapezoidal, excepto que se utiliza la suma del punto medio dos veces en la media. Por lo tanto, si usted ya tiene la suma del punto medio y la suma trapezoidal para algún número de rectángulos o trapecios, puede obtener aproximación regla de Simpson con el promedio simple siguiente:
Por lo tanto, la fórmula anterior implica siempre el mismo número de rectángulos, trapezoides, y la regla de Simpson " trapezoides ".
Si usted no tiene el punto medio y trapezoidales sumas para el acceso directo anteriormente, se puede utilizar la siguiente fórmula para la regla de Simpson.
-
Componer una fotografía en tu iPhone con la regla de los tercios -
Cómo agregar números positivos y negativos con el mismo signo -
Cómo factorizar la suma de dos cubos perfectos - Suma y resta con números negativos
- Aplicando orden de operaciones para expresiones con solamente la suma y resta
-
10 Cosas para recordar acerca de la integración y cálculo
Cálculo II para dummies La siguiente tabla muestra cómo diferenciar e integrar 18 de las funciones más comunes. Como puede ver, la integración invierte diferenciación, devolviendo la función a su estado original, hasta una constante C.La fórmula de Riemann Sum Para…
Encuentra las zonas exactas bajo una curva mediante la integral definida Cuando se aproxima el área bajo una curva utilizando rectángulos, los más rectángulos que utiliza la izquierda, derecha, o punto medio, mejor será la aproximación. Por lo tanto, "todos" que tendría que hacer para conseguir el área exacta…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación Las reglas anti-diferenciación para la integración en gran medida limitar el número de integrales se puede calcular fácilmente. En muchos casos, sin embargo, puede integrar alguna polinomio en tres pasos utilizando la regla de la suma, la Regla…
Cómo aproximar el área del punto medio con rectángulos Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo hacer una aproximación área usando la notación sigma Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
Cómo hacer inaceptables formas aceptables antes de usar l'h & # regla del 244-pital Usted puede utilizar la regla de L'H # de 244-pital de encontrar un límite cuando otros métodos no funcionan. De hecho, incluso si algún otro método funciona, regla de L'H # de 244-pital es a menudo un buen atajo. Si la sustitución del número…
Cómo utilizar la notación sigma para encontrar el área bajo una curva Puede usar la notación sigma para escribir la suma de Riemann para una curva. Esto es útil cuando se quiere derivar la fórmula para el área aproximada bajo la curva. Por ejemplo, digamos que usted desea encontrar el área aproximada de n…
Las reglas básicas de diferenciación Algunas reglas de diferenciación son muy fácil de recordar y utilizar. Estos incluyen la regla constante, regla de la potencia, la regla múltiplo constante, regla de suma, y la regla diferencia.La regla constante: Este es simple. F (X) = 5…