Cómo analizar una serie telescópica
Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:
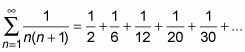
Para ver que ésta es una serie telescópica, usted tiene que utilizar la técnica de fracciones parciales para reescribir
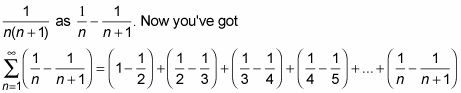
Todos estos términos ahora se derrumban, o telescopio. Los 1 / 2s Cancelar, el 1 / 3s Cancelar, el 1 / 4s cancelan, y así sucesivamente. Todo lo que queda es el primer término, 1 (en realidad, es sólo la mitad de un término), y el último medio plazo,
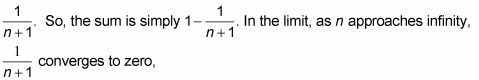
y por lo tanto la suma converge a 1 - 0 o 1.
Usted puede escribir cada término en una serie telescópica como la diferencia de dos medias términos - llamarlos h-términos. A continuación, puede escribir la serie telescópica como
Aquí está la regla de serie telescópica: Una serie telescópica de la forma anterior converge si
entonces la serie diverge.
Esta regla, como la regla para la serie geométrica, le permite determinar qué número de una serie telescópica convergente converge.
-
Los puertos serie en su PC -
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
Libro de Cálculo para dummies -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie converge utilizando la prueba de comparación integral -
La determinación de si una serie de Taylor es convergente o divergente
Expresar y se aproximan a las funciones utilizando la serie de Taylor Es importante entender la diferencia entre eXpressing una función como una serie infinita y lapproximating una función mediante el uso de un número finito de términos de la serie. Usted puede pensar en una serie de potencias como un polinomio…
Expresando funciona como serie de potencias utilizando la serie de Taylor La serie de Taylor proporciona una plantilla para la representación de una amplia variedad de funciones como series de potencias. Es relativamente fácil de trabajar con él, y usted puede adaptarlo para obtener una buena aproximación de muchas…
Expresando funciona como serie de potencias utilizando la serie de Maclaurin los Serie de Maclaurin es una plantilla que le permite expresar muchas otras funciones como series de potencias. Es la fuente de las fórmulas para expresar tanto el pecado X y cos X series como infinito.Sin más preámbulos, aquí está:La…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy…
Cómo utilizar la prueba de raíz para determinar si una serie converge La prueba de la raíz no se puede comparar una nueva serie de una serie de referencia conocido. Su acción consiste en mirar sólo a la naturaleza de la serie que estamos tratando de averiguar. Se utiliza la prueba de raíz para investigar el…