Conexión de una serie con sus dos secuencias relacionadas
Cada serie tiene dos secuencias relacionadas: una secuencia de definición y una secuencia de sumas parciales. La distinción entre una secuencia y una serie es la siguiente:
Una secuencia es una lista de números separados por comas (por ejemplo: 1, 2, 3, ...).
Una serie es una suma de números separados por signos más (por ejemplo: 1 + 2 + 3 + ...).
Cuando ves cómo una serie y sus dos secuencias relacionadas son distintos, pero también relacionado, a obtener una comprensión más clara de cómo el trabajo en serie.
Una serie y su secuencia de definir
La primera secuencia relacionada a una serie es simplemente la secuencia que define la serie en el primer lugar. Por ejemplo, aquí hay tres series escritas tanto en notación sigma y la notación expandida, cada uno emparejado con su secuencia de definir:
Cuando una secuencia {lan} ya está definido, puede utilizar la notación # 8721- lan para referirse a la partida serie relacionada a n = 1. Por ejemplo, cuando
La comprensión de la distinción entre una serie y la secuencia que lo define es importante por dos razones. En primer lugar, y lo más básico, usted no desea conseguir los conceptos de secuencias y series confundido. Pero en segundo lugar, la secuencia que define una serie puede proporcionar información importante acerca de la serie.
Una serie y sus secuencias de sumas parciales
Usted puede aprender mucho acerca de una serie mediante la búsqueda de la sumas parciales de sus primeros términos. Por ejemplo, aquí hay una serie que has visto antes:
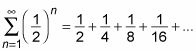
Y aquí están los primeros cuatro sumas parciales de esta serie:
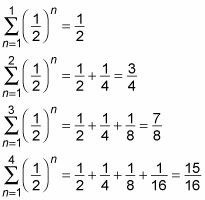
Usted puede convertir las sumas parciales de esta serie en una secuencia de la siguiente manera:
En general, todas las series # 8721- lan tiene una secuencia relacionada de sumas parciales {Sn}. Por ejemplo, aquí hay algunos dichos emparejamientos:
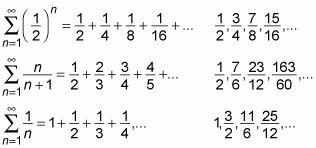
Recuerde que cada serie y su secuencia relacionada de sumas parciales son o bien tanto convergente o tanto divergente. Por otra parte, si los dos son convergentes, ambos convergen en el mismo número.
Esta regla no debería ser una gran sorpresa. Después de todo, una secuencia de sumas parciales simplemente le da un total acumulado de donde una serie va. Sin embargo, esta regla puede ser útil. Por ejemplo, suponga que desea saber si la siguiente secuencia es convergente o divergente:
¿Qué diablos es esta secuencia, de todos modos? Tras un examen más profundo, sin embargo, usted descubrirá que es la secuencia de sumas parciales de una serie muy simple:
Esta serie, llamada serie armónica, es divergente, por lo que se puede concluir que su secuencia de sumas parciales también diverge.
-
Opciones del menú Formato en la TI-83 Plus -
Guardar y dibujar gráficos de secuencia en la TI-83 Plus -
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
Cómo graficar secuencias y diagramas de fase en TI-Nspire -
Comparando convergentes y divergentes secuencias -
La determinación de si una serie de Taylor es convergente o divergente
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo calcular los términos de un secuencia mediante el uso de la expresión secuencia Si te dan unos términos de una secuencia, a menudo se pueden usar estos términos para encontrar la fórmula general para la secuencia. Si te dan la fórmula general (completo con n como la variable), se encuentra el nº término de la sucesión…
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
¿Cómo encontrar la suma parcial de una secuencia aritmética Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula…
¿Cómo encontrar la suma parcial de una secuencia geométrica Cuando su profesor de pre-cálculo le pide que encontrar la suma parcial de una secuencia geométrica, la suma tendrá un límite superior y un límite inferior. La razón común de sumas parciales de este tipo no tiene restricciones…
¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
¿Cómo reconocer secuencias aritméticas recursivas LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia Notación de sumatoria es una forma útil para representar la suma parcial de una secuencia. La suma de la primera k términos de una progresión aritmética se conoce como la ksuma parcial TH. Se llaman sumas parciales porque sólo eres capaz de…