¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica
Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r lt; 1, lan crece sin límite infinito, así que no hay límite sobre cuán grande es el valor absoluto de lan (|lan|) Pueden obtener. Si |r| lt; 1, para cada valor de n, |rn| continúa disminuyendo infinitamente hasta que se convierte arbitrariamente cerca de 0. Esta disminución se debe a que cuando multiplicas una fracción entre -1 y 1 por sí misma, el valor absoluto de esa fracción continúa consiguiendo más pequeño hasta que se vuelve tan pequeño que apenas se note. Por lo tanto, el término rk casi desaparece por completo en la fórmula suma geométrica finita:
Y si el rk desaparece - o se pone muy pequeña - las fórmulas cambios finitos a la siguiente y le permite encontrar la suma de una serie geométrica infinita:
Por ejemplo, siga los pasos para encontrar este valor:
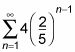
Encuentra el valor de la1 enchufando 1 para n.
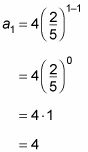
Calcular la2 mediante la conexión de 2 de n.
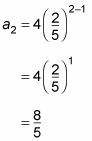
Determinar r.
Encontrar r, divides la2 por la1:
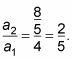
Plug la1 y r en la fórmula para encontrar la suma infinita.
Enchufe y simplificar para encontrar lo siguiente:
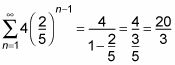
Repetición de decimales también se pueden expresar como sumas infinitas. Considere el número 0,5555555. . . . Usted puede escribir este número como 0,5 + 0,05 + 0,005 +. . . , Y así sucesivamente para siempre. El primer término de esta secuencia se 0.5- encontrar r, 0,05 dividido por 0,5 = 0,1.
Conecte estos valores en la fórmula infinita suma:
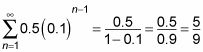
Tenga en cuenta que esta suma es finita sólo si r se encuentra estrictamente entre -1 y 1.
-
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
Encontrar la suma y diferencia de los dos mismos términos -
Cómo determinar el valor absoluto -
Encontrar el valor absoluto de un número -
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular los términos de un secuencia mediante el uso de la expresión secuencia
¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética Si conoces a los primeros términos de una progresión aritmética, puede escribir una expresión general para la secuencia para encontrar el nº plazo. Para escribir la expresión general, debe buscar un patrón en los primeros términos de la…
¿Cómo encontrar la suma parcial de una secuencia aritmética Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula…
¿Cómo encontrar la suma parcial de una secuencia geométrica Cuando su profesor de pre-cálculo le pide que encontrar la suma parcial de una secuencia geométrica, la suma tendrá un límite superior y un límite inferior. La razón común de sumas parciales de este tipo no tiene restricciones…
¿Cómo encontrar la tangente de la suma o diferencia de ángulos Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el…
Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…
Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…
¿Cómo reconocer secuencias aritméticas recursivas LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…
Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…
Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia Notación de sumatoria es una forma útil para representar la suma parcial de una secuencia. La suma de la primera k términos de una progresión aritmética se conoce como la ksuma parcial TH. Se llaman sumas parciales porque sólo eres capaz de…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
¿Cómo encontrar la media geométrica ponderada de un conjunto de datos Cuando un conjunto de datos contiene un gran número de valores repetidos, se puede simplificar el proceso de cálculo de la media mediante el uso de pesos - las frecuencias de un valor en una muestra o una población. A continuación, puede…
Cómo trabajar y verificar integral de convolución y resumir los problemas El dominio de las integrales de convolución y sumas viene a través de la práctica. Aquí hay soluciones detalladas de análisis a un solo integral de convolución y dos sumas de convolución problemas, cada uno seguido de verificaciones…