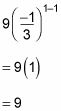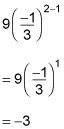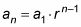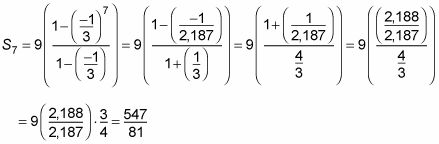¿Cómo encontrar la suma parcial de una secuencia geométrica
Cuando su profesor de pre-cálculo le pide que encontrar la suma parcial de una secuencia geométrica, la suma tendrá un límite superior y un límite inferior. La razón común de sumas parciales de este tipo no tiene restricciones específicas.
Puede encontrar la suma parcial de una secuencia geométrica, que tiene la expresión explícita general de
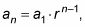
mediante el uso de la siguiente fórmula:
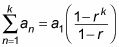
Por ejemplo, para encontrar
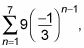
sigue estos pasos:
Encontrar la1 enchufando 1 para n.
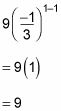
Encontrar la2 mediante la conexión de 2 de n.
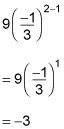
Dividir la2 por la1 encontrar r.
Para este ejemplo, r = -3/9 = -1/3. Observe que este valor es el mismo que la fracción en el paréntesis.
Usted puede haber notado que 9 (-1/3)n - 1 sigue la fórmula general para
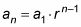
(la fórmula general para una secuencia geométrica) exactamente, donde la1 = 9 y r = -1/3. Sin embargo, si no te diste cuenta que, el método utilizado en los pasos 1.3 funciona a la perfección.
Plug la1, r, y k en la fórmula suma.
El problema ahora se reduce a las siguientes simplificaciones:
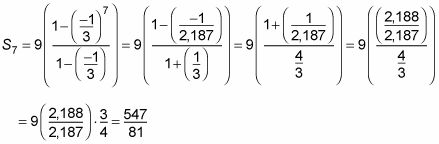
Problemas de suma geométricos toman un poco de trabajo con fracciones, así que asegúrese de encontrar un denominador común, invertir, y se multiplican cuando sea necesario. O puede usar una calculadora y luego reconvertir a una fracción. Sólo tenga cuidado al utilizar paréntesis correctos al introducir los números.
-
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
¿Cómo encontrar la suma de fracciones con el mismo denominador -
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo analizar la convergencia absoluta y condicional -
Cómo calcular los términos de un secuencia mediante el uso de la expresión secuencia -
Cómo calcular el seno de ángulos especiales en grados
Cómo calcular el seno de ángulos especiales en radianes Usted puede utilizar el concepto de fórmulas de suma y diferencia para calcular el seno de ángulos especiales en radianes. Este proceso es diferente a la resolución de ecuaciones porque aquí se le pedirá que encontrar el valor trigonométrica…
¿Cómo encontrar la fórmula general para el enésimo término de una sucesión aritmética utilizando cualquiera de los dos términos En algún momento, su profesor de pre-cálculo le pedirá que encontrar la fórmula general para la nº período de una sucesión aritmética sin conocer el primer término o la diferencia común. En este caso, se le dará dos términos (no…
¿Cómo encontrar el enésimo término utilizando los primeros términos de una progresión aritmética Si conoces a los primeros términos de una progresión aritmética, puede escribir una expresión general para la secuencia para encontrar el nº plazo. Para escribir la expresión general, debe buscar un patrón en los primeros términos de la…
¿Cómo encontrar la suma parcial de una secuencia aritmética Cuando su profesor de pre-cálculo pide a calcular la kº suma parcial de una secuencia aritmética, es necesario agregar el primer k términos. Esto puede tardar un poco, sobre todo si k es largo. Afortunadamente, usted puede utilizar una fórmula…
¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…
¿Cómo encontrar la tangente de la suma o diferencia de ángulos Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el…
Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…
Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…
¿Cómo reconocer secuencias aritméticas recursivas LA secuencia recursiva es una secuencia aritmética en la que cada término depende del plazo (s) antes de IT- la secuencia de Fibonacci es un ejemplo bien conocido. Cuando su profesor de pre-cálculo le pide que encontrar cualquier término en una…
Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…
Cómo utilizar la notación de sumatoria para mostrar una suma parcial de una secuencia Notación de sumatoria es una forma útil para representar la suma parcial de una secuencia. La suma de la primera k términos de una progresión aritmética se conoce como la ksuma parcial TH. Se llaman sumas parciales porque sólo eres capaz de…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…