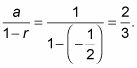Cómo analizar la convergencia absoluta y condicional
Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:
Pero, si cambia cualquier otro signo a negativo, se obtiene el alternando serie armónica, que converge:
Por cierto, esta serie converge a ln 2, lo que equivale a alrededor de 0,6931.
Una serie alternante se dice que es condicionalmente convergente si es convergente, ya que es, pero se convertiría divergente si todos sus términos se hicieron positiva. Una serie alternante se dice que es absolutamente convergente si sería convergente incluso si todos sus términos se hicieron positiva. Y cualquier dicha serie absolutamente convergente también es convergente automáticamente tal como es.
He aquí un ejemplo. Determinar la convergencia o divergencia de la siguiente serie alternante:
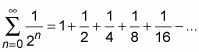
Si todos estos términos fueron positivos, tendrías la serie geométrica familiar,
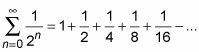
que, por regla serie geométrica, converge a 2. Debido a la serie positiva converge, la serie alterna también debe converger y que decir que la serie alterna es absolutamente convergente.
El hecho de que la convergencia absoluta implica la convergencia ordinaria es sólo sentido común, si se piensa en ello. La serie geométrica anterior de términos positivos converge a 2. Si ha realizado todos los términos negativos, sería sumar a -2, ¿verdad? Así que, si algunos de los términos son positivos y otros negativos, la serie debe converger a algo entre -2 y 2.
¿Te diste cuenta de que la serie alternada de arriba es una serie geométrica tal cual con
(Recordemos que la fórmula para la suma de una serie geométrica funciona siempre r está entre -1 y 1- Por lo tanto, funciona para la serie alterna, así como para la serie positivo) La fórmula da su suma.:
-
Los puertos serie en su PC -
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
Libro de Cálculo para dummies -
Comparando convergentes y divergentes secuencias -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie converge utilizando la prueba de comparación integral
La determinación de si una serie de Taylor es convergente o divergente Debido a que la serie de Taylor es una forma de series de potencias, cada serie de Taylor también tiene un intervalo de convergencia. Cuando este intervalo es todo el conjunto de los números reales, se puede utilizar la serie para encontrar el…
Expresar y se aproximan a las funciones utilizando la serie de Taylor Es importante entender la diferencia entre eXpressing una función como una serie infinita y lapproximating una función mediante el uso de un número finito de términos de la serie. Usted puede pensar en una serie de potencias como un polinomio…
Expresando la función sen x como una serie Si usted quiere encontrar el valor aproximado del pecado X, puede utilizar una fórmula para expresarlo como una serie. Esta fórmula expresa la función seno como una serie alternante:Para darle sentido a esta fórmula, utilice la notación…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy…
Cómo utilizar la prueba de raíz para determinar si una serie converge La prueba de la raíz no se puede comparar una nueva serie de una serie de referencia conocido. Su acción consiste en mirar sólo a la naturaleza de la serie que estamos tratando de averiguar. Se utiliza la prueba de raíz para investigar el…
¿Cómo trabajar con series geométricas Series geométricas son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. Una serie geométrica es una serie de la forma:El primer…