¿Cómo trabajar con series geométricas
Series geométricas son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. Una serie geométrica es una serie de la forma:
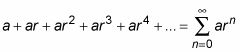
El primer término, la, se llama la término principal. Cada término después de la primera es igual al plazo anterior, multiplicado por r, que se llama la común proporción.
Por ejemplo, si la es 5 y r es 3, se obtiene
Usted acaba de multiplicar cada término por 3 para obtener el próximo mandato. Por cierto, la 3 en este ejemplo es el llamado común proporción debido a que la relación de cualquier término dividido por su término anterior es igual a 3, pero es probable que tenga mucho más sentido pensar en el 3 como su multiplicador.
Si la es 100 y r es 0.1, se obtiene
Y si la es un medio y r también es un medio, se obtiene la serie:
La regla de convergencia / divergencia de la serie geométrica es un broche de presión.
Regla de la serie geométrica:
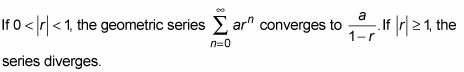
(Tenga en cuenta que esta regla funciona cuando -1 # 60- r # 60- 0, en cuyo caso se obtiene una alterno serie.)
En el primer ejemplo, la = 5 y r = 3, por lo que la serie diverge. En el segundo ejemplo, la es 100 y r es 0,1, por lo que la serie converge a
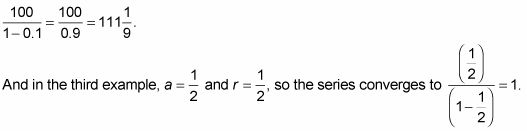
Esta es la distancia que camina si comienza a 1 yarda de la pared, luego paso a mitad de camino a la pared, y luego la mitad de la distancia restante, y así sucesivamente y así sucesivamente. Se toma un número infinito de pasos, pero viaja un simple patio. ¿Y cuánto tiempo le tomará para llegar a la pared? Bueno, si se mantiene una velocidad constante y no una pausa entre los pasos (que por supuesto es imposible), obtendrá allí en la misma cantidad de tiempo que le tomaría a caminar cualquier de edad patio. Si pausa entre los pasos, incluso para una milmillonésima parte de un segundo, se le nunca llegar a la pared.
-
Gráfico sumas parciales de una serie infinita de la TI-84 Plus -
Libro de Cálculo para dummies -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie converge utilizando la prueba de comparación integral -
La determinación de si una serie de Taylor es convergente o divergente -
Expresar y se aproximan a las funciones utilizando la serie de Taylor
Expresando funciona como serie de potencias utilizando la serie de Taylor La serie de Taylor proporciona una plantilla para la representación de una amplia variedad de funciones como series de potencias. Es relativamente fácil de trabajar con él, y usted puede adaptarlo para obtener una buena aproximación de muchas…
Expresando funciona como serie de potencias utilizando la serie de Maclaurin los Serie de Maclaurin es una plantilla que le permite expresar muchas otras funciones como series de potencias. Es la fuente de las fórmulas para expresar tanto el pecado X y cos X series como infinito.Sin más preámbulos, aquí está:La…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo encontrar el valor de una suma infinita en una secuencia geométrica Si tu profesor de pre-cálculo le pide que encontrar el valor de una suma infinita en una secuencia geométrica, el proceso es muy simple - siempre y cuando usted mantenga sus fracciones y decimales recta. Si r se encuentra fuera del rango -1 lt; r…
Cómo identificar un término en una secuencia geométrica cuando sabes mandatos consecutivos Si tu profesor de pre-cálculo le da mandatos consecutivos en una secuencia geométrica y le pide que identifique un nuevo mandato en la secuencia, los pasos que deberá seguir para encontrar este término son muy similares a los de las secuencias…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…