Cómo determinar si una serie alternante converge o diverge
Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:
Su nº término converge a cero.
Sus términos son no aumentando - en otras palabras, cada término es ya sea menor o igual que su predecesor (ignorando los signos menos).
El uso de esta sencilla prueba, usted puede demostrar fácilmente muchas series alternando ser convergente. Los términos sólo tienen que converger a cero y obtener más y más pequeño (que rara vez siendo el mismo). La serie armónica alternada converge con esta prueba:
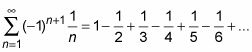
Como hacer las dos series siguientes:
El Criterio de Leibniz Sólo se puede decir que una misma serie alternada converge. La prueba no dice nada acerca de la serie positiva plazo. En otras palabras, la prueba no se puede decir si una serie es absolutamente convergente o condicionalmente convergente. Para responder a esta pregunta, debe investigar la serie positiva con una prueba diferente. (Si la serie alterna es convergente, ya que es, tiene que ser en términos absolutos o condicionalmente convergent- es sólo que no puede determinar cual es menos que seas capaz de averiguar si es o no la serie positiva plazo converge.)
Ahora intente el siguiente problema. Determinar la convergencia o divergencia de la serie siguiente. Si convergente, determinar si la convergencia es condicional o absoluta.
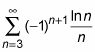
Compruebe que el nº término converge a cero.
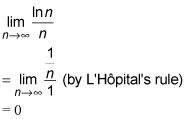
Compruebe siempre la nº término primero porque si no converge a cero, ya está hecho - la serie alterna y la serie positiva tanto divergir. Tenga en cuenta que la nprueba º período de divergencia se aplica a la serie alterna, así como la serie positiva.
Compruebe que los términos disminuyen o permanecen igual (haciendo caso omiso de los signos menos).
Esto es negativo para todos X # 8805- 3 (porque el logaritmo natural de cualquier cosa 3 o superior es más de 1 y X-cuadrado, por supuesto, siempre es positiva), por lo que la derivada y por tanto la pendiente de la función son negativos, y por lo tanto la función es decreciente. Por último, debido a que la función es decreciente, los términos de la serie también están disminuyendo. (Recordemos que haciendo caso omiso de cualquier número de términos en el comienzo de una serie no afecta si la serie converge o diverge o si la convergencia es condicional o absoluto- es por eso que está bien para empezar X = 3 y n = 3.) que lo hace.
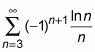
converge por el Criterio de Leibniz.
Determinar el tipo de convergencia.
Se puede ver que para n # 8805- 3 la serie positivo,
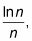
es mayor que la serie armónica divergente,
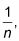
por lo que la serie positiva diverge por la prueba de comparación directa. Por lo tanto, la serie alterna es condicionalmente convergente.
Si la serie alterna no satisface el segundo requisito de la prueba de serie alternante, lo hace no se sigue que la serie diverge, solo que esta prueba no demuestra la convergencia.
-
Los puertos serie en su PC -
Libro de Cálculo para dummies -
Comparando convergentes y divergentes secuencias -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie converge utilizando la prueba de comparación integral -
La determinación de si una serie de Taylor es convergente o divergente
Expresar y se aproximan a las funciones utilizando la serie de Taylor Es importante entender la diferencia entre eXpressing una función como una serie infinita y lapproximating una función mediante el uso de un número finito de términos de la serie. Usted puede pensar en una serie de potencias como un polinomio…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy…
Cómo utilizar la prueba de raíz para determinar si una serie converge La prueba de la raíz no se puede comparar una nueva serie de una serie de referencia conocido. Su acción consiste en mirar sólo a la naturaleza de la serie que estamos tratando de averiguar. Se utiliza la prueba de raíz para investigar el…
¿Cómo trabajar con series geométricas Series geométricas son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. Una serie geométrica es una serie de la forma:El primer…
¿Cómo clasificar las tendencias en un modelo de regresión de series de tiempo Para estimar una serie de tiempo con el análisis de regresión, el primer paso es identificar el tipo de tendencia (si los hay) que está presente en los datos. El tipo de tendencia, tales como lineal o cuadrática, determina la ecuación exacta…