Cómo utilizar la prueba de comparación límite para determinar si una serie converge

La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador es, por ejemplo, 100 o 10 000, o 1 / 10.000, ya que cualquier número, grande o pequeño, los tiempos de la suma finita de la serie original es todavía un número finito. Lo mismo va para una serie divergente multiplicado por cualquier número. Esa nueva serie también diverge porque cualquier número, grande o pequeño, los tiempos de infinito sigue siendo infinito. Esto es más simplificada - es sólo en el límite que una serie es una especie de un múltiplo de la otra - pero transmite el principio básico.

Puede descubrir si existe tal conexión entre dos series examinado la relación de la nth términos de las dos series como n tiende a infinito. Aquí está la prueba.

Comparación Límite Test: Para dos series,

dónde L es finito y positivo, o bien ambas series convergen o ambas divergen.

Esta es una buena prueba para utilizar cuando no se puede usar la prueba de comparación directa para su serie, ya que va por el camino equivocado - en otras palabras, su serie es más grande que una conocida convergente series o menor que una conocida divergente serie.

He aquí un ejemplo: ¿Tiene

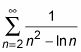
converger o divergir? Esta serie se asemeja a la convergente p-serie

así que ese es su punto de referencia. Pero no se puede utilizar la prueba de comparación directa debido a que los términos de su serie son más grandes que

En su lugar, se utiliza la prueba de comparación límite.

Tome el límite de la relación de la nth términos de las dos series. No importa que la serie se pone en el numerador y el que en el denominador, pero si pones lo conocido, la serie de referencia en el denominador, esto hace que sea un poco más fácil hacer estos problemas y para comprender los resultados.

Debido a que el límite es finito y positivo, y debido a la serie de referencia converge, su serie también debe converger.

Por lo tanto,

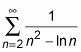
converge.

Probemos otro ejemplo. Determinar la convergencia o divergencia de

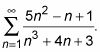
La prueba de comparación límite es un buen año para la serie, como éste, en el que el término general es una racional función - en otras palabras, donde el término general es un cociente de dos polinomios.

1. Determine la serie de referencia.

   Tome la mayor potencia de n en el numerador y el denominador - ignorando cualquier coeficientes y todos los demás términos - entonces simplificar. Me gusta esto:

   

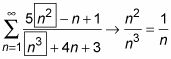
   La serie de referencia es, pues,

   

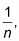
   el divergente serie armónica.

2. Tome el límite de la relación de la nth términos de las dos series.

   

3. Debido a que el límite de la Etapa 2 es finito y positivo, y porque la serie de referencia diverge, su serie también debe divergir.

   Por lo tanto,

   

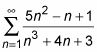
   diverge.

Contrariamente a la definición formal de la prueba de comparación Limit (al principio de este artículo), el límite, L, no tiene que ser finita y positiva para la prueba de trabajar. En primer lugar, si la serie de referencia es convergente, y lo pones en el denominador del límite, y el límite es cero, entonces su serie también debe converger. Si el límite es el infinito, no se puede concluir nada. Y en segundo lugar, si la serie de referencia es divergente, y lo puso en el denominador, y el límite es infinito, entonces su serie debe también divergen. Si el límite es cero, se aprende nada.