Cómo utilizar la prueba de raíz para determinar si una serie converge
La prueba de la raíz no se puede comparar una nueva serie de una serie de referencia conocido. Su acción consiste en mirar sólo a la naturaleza de la serie que estamos tratando de averiguar. Se utiliza la prueba de raíz para investigar el límite de la nTH raíz de la nº plazo de su serie. Al igual que con la prueba de razón, si el límite es menor que 1, el converges- serie si se trata de más de 1 (incluyendo el infinito), el diverges- serie y si el límite es igual a 1, se aprende nada.
La prueba de raíz es una buena para probar si la serie implica npoderes ª.
Pruebe esto: ¿El
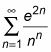
converger o divergir? Esto es lo que hace:
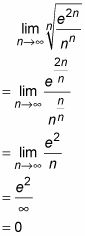
Debido a que el límite es inferior a 1, la serie converge.
A veces es útil hacer una conjetura sobre la convergencia o divergencia de una serie antes de lanzarse a una o más de las pruebas de convergencia / divergencia. He aquí un consejo que ayuda con algunas series. Las siguientes expresiones se enumeran de " más pequeño " a " # 148 ;: mayor
(El 10 es un número- arbitraria el tamaño del número no afecta a este orden). Una serie con una " más pequeño " expresión sobre un " grande " un solo converge, por ejemplo,
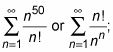
y una serie con una " grande " expresión sobre un " más pequeño " un solo diverge, por ejemplo,