Cómo utilizar la prueba enésimo plazo para determinar si una serie converge
Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy prueba fácil de usar.
los nª Prueba de Término:
(Probablemente descubierto que con este símbolo sumatorio desnudo, n va desde el 1 hasta el infinito.)
Si lo piensas bien, esto es sólo sentido común. Cuando una serie converge, la suma de todos los términos se Poniendo a punto en un cierto número. La única manera que esto puede suceder es cuando los números están agregando en el extremo " # 148 final; de la serie están recibiendo infinitamente pequeño - como en la serie:
Imagínese, en cambio, que los términos de una serie están convergiendo, digamos, a 1, como en la serie
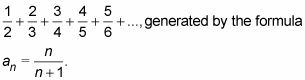
En ese caso, cuando se suman los términos, sigues añadiendo números muy cercanos a 1 una y otra y otra vez para siempre - y esto debe añadir hasta el infinito. Así, para una serie a converger, los términos de la serie deben converger a cero. Pero asegúrese de que entiende lo que esto nprueba ª término hace no decir.
Cuando los términos de una serie convergen a cero, eso no garantiza que la serie converge. En logicianese hifalutin - el hecho de que los términos de una serie convergen a cero es un necesario pero no suficiente condición para concluir que la serie converge a una suma finita.
Debido a que esta prueba suele ser muy fácil de aplicar, debe ser una de las primeras cosas que comprueba cuando se trata de determinar si una serie converge o diverge. Por ejemplo, si se le pregunta para determinar si
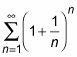
converge o diverge, tenga en cuenta que cada término de esta serie es un número mayor que 1 se eleva a una potencia positiva. Esto siempre se traduce en un número mayor que 1, y por lo tanto, los términos de esta serie no convergen a cero, y por lo tanto la serie debe divergir.
los nprueba ª término no sólo funciona para la serie positiva ordinaria, sino que también trabaja para la serie de términos positivos y negativos.
-
Los puertos serie en su PC -
Libro de Cálculo para dummies -
Conexión de una serie con sus dos secuencias relacionadas -
La determinación de si una serie converge utilizando la prueba de comparación integral -
La determinación de si una serie de Taylor es convergente o divergente -
Expresar y se aproximan a las funciones utilizando la serie de Taylor
Expresando funciona como serie de potencias utilizando la serie de Maclaurin los Serie de Maclaurin es una plantilla que le permite expresar muchas otras funciones como series de potencias. Es la fuente de las fórmulas para expresar tanto el pecado X y cos X series como infinito.Sin más preámbulos, aquí está:La…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba de raíz para determinar si una serie converge La prueba de la raíz no se puede comparar una nueva serie de una serie de referencia conocido. Su acción consiste en mirar sólo a la naturaleza de la serie que estamos tratando de averiguar. Se utiliza la prueba de raíz para investigar el…
¿Cómo trabajar con series geométricas Series geométricas son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. Una serie geométrica es una serie de la forma:El primer…
Seno y coseno con el álgebra Usted puede aproximar, con bastante precisión, el seno y el coseno de ángulos con un infinito serie, que es la suma de los términos de una secuencia o lista, de los números. Tome en cuenta, sin embargo, que la serie de seno y coseno son exactos…