Expresar y se aproximan a las funciones utilizando la serie de Taylor
Es importante entender la diferencia entre eXpressing una función como una serie infinita y lapproximating una función mediante el uso de un número finito de términos de la serie. Usted puede pensar en una serie de potencias como un polinomio con un número infinito de términos (Taylor polinómicas).
Cada serie de Taylor proporciona el valor exacto de una función para todos los valores de X donde la serie converge. Es decir, para cualquier valor de X en su intervalo de convergencia, una serie de Taylor converge a F(X).
Aquí está la serie de Taylor en todo su esplendor:
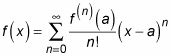
En la práctica, sin embargo, la suma de un número infinito de términos, simplemente no es posible. Sin embargo, se puede aproximar el valor de F(X) Mediante la adición de un número finito de la serie de Taylor apropiado.
Una expresión construido a partir de un número finito de términos de una serie de Taylor se llama Polinomio de Taylor, Tn(X). Al igual que otros polinomios, un polinomio de Taylor se identifica por su grado. Por ejemplo, aquí está el quinto grado del polinomio de Taylor, T5(X), Que se aproxima eX:
En términos generales, un mayor grado resultados polinomio en una mejor aproximación. Para el valor de eX cuando X es cerca de 100, se obtiene una buena estimación utilizando un polinomio de Taylor de eX con la = 100:
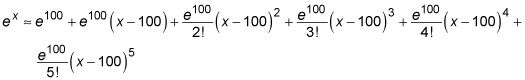
En resumen, recuerde lo siguiente:
Una serie de Taylor convergente expresa el valor exacto de una función.
Un polinomio de Taylor, Tn(X), De una serie convergente se aproxima al valor de una función.
-
Cómo eliminar datos sql obsoletos -
Cálculo de límites de error para taylor polinomios -
La determinación de si una serie de Taylor es convergente o divergente -
Expresando funciona como serie de potencias utilizando la serie de Taylor -
Expresando funciona como serie de potencias utilizando la serie de Maclaurin -
Expresando las cos función x como una serie
Expresando la función sen x como una serie Si usted quiere encontrar el valor aproximado del pecado X, puede utilizar una fórmula para expresarlo como una serie. Esta fórmula expresa la función seno como una serie alternante:Para darle sentido a esta fórmula, utilice la notación…
Factoring cuatro o más términos agrupando Cuando un polinomio tiene cuatro o más términos, la forma más fácil de factorizar que es usar agrupación. En este método, nos fijamos en sólo dos términos a la vez para ver si cualquiera de las técnicas se hacen evidentes. Por ejemplo,…
Cómo analizar una serie telescópica Usted no ve muchas series telescópica, pero la regla serie telescópica es buena para mantener en su bolsa de trucos - nunca se sabe cuando puede ser útil. Considere las siguientes series:Para ver que ésta es una serie telescópica, usted tiene…
Cómo analizar la convergencia absoluta y condicional Muchas series divergentes de términos positivos convergen si cambia las señales de sus condiciones de forma que alternan entre positivo y negativo. Por ejemplo, usted sabe que la serie armónica diverge:Pero, si cambia cualquier otro signo a…
Cómo analizar una serie p El llamado p-series son series relativamente simple, pero importante, que se puede utilizar como puntos de referencia para determinar la convergencia o divergencia de la serie más complicada. LA p-serie es de la forma(dónde p es un positivo…
Cómo determinar si una serie alternante converge o diverge Un alterno serie es una serie donde los términos alternan entre positivo y negativo. Se puede decir que una serie alternante converge si se cumplen dos condiciones:Su nº término converge a cero.Sus términos son no aumentando - en otras palabras,…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo reconocer una serie p Un tipo importante de serie se llama la p-serie. LA p-serie puede ser divergente o convergente, en función de su valor. Se toma la siguiente forma:He aquí un ejemplo común de un p-serie, cuando p = 2:Aquí hay algunos otros ejemplos de…
Cómo comprobar si una serie converge o diverge Digamos que usted está tratando de averiguar si una serie converge o diverge, pero no se ajusta a ninguna de las pruebas que conoces. Sin preocupaciones. Usted encontrará una serie de referencia que usted sabe converge o diverge y luego comparar…
Cómo utilizar la prueba de comparación límite para determinar si una serie converge La idea detrás de la prueba de comparación de límite es que si usted toma una serie convergente conocido y se multiplica cada uno de sus términos por algún número, luego que la nueva serie también converge. Y no importa si el multiplicador…
Cómo utilizar la prueba enésimo plazo para determinar si una serie converge Si los términos individuales de una serie (en otras palabras, los términos de secuencia subyacente de la serie) no convergen a cero, entonces la serie debe divergir. Este es el nprueba ª plazo para la divergencia. Esto es por lo general una muy…
Cómo utilizar las raíces de un polinomio para encontrar sus factores los factor de teorema indica que usted puede ir y venir entre las raíces de un polinomio y los factores de un polinomio. En otras palabras, si usted conoce uno, ya sabes el otro. A veces, su maestro o su libro de texto pueden pedirle que factorizar…