Cálculo de límites de error para taylor polinomios
Un polinomio de Taylor se aproxima al valor de una función, y en muchos casos, es útil para medir la exactitud de una aproximación. Esta información es proporcionada por el Taylor plazo restante:
F(X) = Tn(X) + Rn(X)
Tenga en cuenta que la adición del término restante Rn(X) Convierte a la aproximación en una ecuación. Aquí está la fórmula para el término restante:
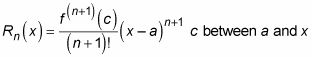
Es importante tener claro que esta ecuación se cumple para un solo específico valor de c en el intervalo entre la y X. Lo hace no trabajar para cualquier valor de c en ese intervalo.
Idealmente, el término resto le da la diferencia precisa entre el valor de una función y la aproximación Tn(X). Sin embargo, debido a que el valor de c es incierto, en la práctica, el término resto realmente ofrece un escenario peor de los casos para su aproximación.
El siguiente ejemplo debería ayudar a hacer que esta idea clara, utilizando el sexto grado del polinomio de Taylor para cos X:
Supongamos que usted usa este polinomio para aproximar cos 1:
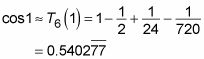
¿Qué tan precisa es esta aproximación probable que sea? Para averiguarlo, usar el término restante:
cos 1 = T6(X) + R6(X)
Adición de los restantes asociados cambios a largo plazo esta aproximación en una ecuación. Aquí está la fórmula para el término restante:
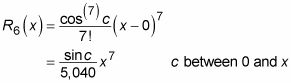
Así sustituyendo 1 para X te dio:
En este punto, usted es aparentemente atascado, porque usted no sabe el valor del pecado c. Sin embargo, usted puede conectar c = 0 y c = 1 para darle un rango de valores posibles:
Tenga en cuenta que esta desigualdad se debe a que el intervalo involucrados, y debido a que aumenta el seno de ese intervalo. Usted puede obtener una cota diferente con un intervalo diferente.
Esto simplifica para proporcionar una aproximación muy cercana:
Así, el término resto predice que el valor aproximado calculado anteriormente estará dentro de 0,00017 del valor real. Y, de hecho,
Como puede ver, la aproximación se encuentra dentro de los límites de error previstos por el término restante.
-
3 Principales modelo de probabilidad lineal (lpm) problemas -
Los fundamentos de la resolución de ecuaciones de álgebra i -
1.001 problemas de la práctica de Cálculo para los maniquíes -
La determinación de si una serie de Taylor es convergente o divergente -
Expresar y se aproximan a las funciones utilizando la serie de Taylor -
Expresando funciona como serie de potencias utilizando la serie de Taylor
Expresando funciona como serie de potencias utilizando la serie de Maclaurin los Serie de Maclaurin es una plantilla que le permite expresar muchas otras funciones como series de potencias. Es la fuente de las fórmulas para expresar tanto el pecado X y cos X series como infinito.Sin más preámbulos, aquí está:La…
Expresando las cos función x como una serie Si usted quiere encontrar el valor aproximado de cos X, usted comienza con una fórmula que expresa el valor del pecado X para todos los valores de X como una serie infinita. Diferenciando ambos lados de esta fórmula conduce a una fórmula similar…
Expresando la función sen x como una serie Si usted quiere encontrar el valor aproximado del pecado X, puede utilizar una fórmula para expresarlo como una serie. Esta fórmula expresa la función seno como una serie alternante:Para darle sentido a esta fórmula, utilice la notación…
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Cómo aproximar área con la regla de Simpson Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson…
¿Cómo encontrar un factor común más grande de un polinomio No importa cuántos términos de un polinomio tiene, uno siempre quiere comprobar si hay un máximo común divisor (MCD) en primer lugar. Si el polinomio tiene un GCF, factoring el resto del polinomio es mucho más fácil porque una vez que se toma…
¿Cómo encontrar raíces imaginarias usando el teorema fundamental del álgebra El teorema fundamental del álgebra puede ayudarle a encontrar las raíces imaginarias. Raíces imaginarias aparecerá en una ecuación de segundo grado cuando el discriminante de la ecuación de segundo grado - la parte bajo el signo de la raíz…
¿Cómo encontrar las raíces reales de un polinomio utilizando la regla de los signos de Descartes Si sabe el número de raíces totales un polinomio tiene, puede utilizar un teorema muy bien llamada Regla de los signos de Descartes a contar cuántas raíces son números reales (tanto positivos y negativa) y cuántos son imaginarios. Usted ve, el…
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
Cómo identificar un término en una secuencia geométrica cuando sabes dos mandatos no consecutivos Si tu profesor de pre-cálculo le da dos términos no consecutivos de una secuencia geométrica, se puede encontrar la fórmula general de la secuencia, así como cualquier término especificado. Por ejemplo, si el quinto término de una secuencia…
Cómo hacer aproximaciones lineales Debido a que las funciones ordinarias son localmente lineal (que significa recto) - y cuanto más te acercas a ellos, el más recto que buscar-una línea tangente a una función es una buena aproximación de la función cerca del punto de…
Cómo usar términos consecutivos de encontrar otro en una secuencia aritmética Si tu profesor de pre-cálculo le da dos términos consecutivos de una progresión aritmética y le pide que encontrar otro, puede utilizar una fórmula general para encontrar la diferencia común entre estos términos. Por ejemplo, una secuencia…