Muchas personas primero se encuentran con los límites siguientes en un libro de texto de cálculo cuando se trata de probar las fórmulas derivadas de la función seno y la función coseno. Estos resultados no son inmediatamente obvias y en realidad tienen un poco de trabajo de justificar. Cualquier texto de cálculo debe ofrecer más explicaciones si usted está interesado en verlo!
1.001 problemas de la práctica de Cálculo para los maniquíes
Los siguientes son algunos de los más frecuentemente utilizados teoremas, fórmulas y definiciones que te encuentres en una clase de cálculo para una sola variable. La lista no es exhaustiva, sino que debe cubrir los elementos que va a utilizar con más frecuencia.
Conteúdo
- Límite definición de un derivado
- Definición: continua a un número la
- El teorema del valor intermedio
- Definición de un número crítico
- Teorema de rolle
- El teorema del valor medio
- De newton método de aproximación fórmula
- El teorema fundamental del cálculo
- La regla del trapezoide
- Regla de simpson
- Fórmulas especiales límite de cálculo
- Fórmulas derivados y de integración para funciones hiperbólicas
Límite Definición de un Derivado
Definición: continua a un número la
El teorema del valor intermedio
Definición de un Número crítico
LA número crítico de una función F es un número c en el dominio de F de tal manera que ya sea F '(c) = 0 o F '(c) no existe.
Teorema de Rolle
Dejar F ser una función que satisface las tres hipótesis siguientes:
F es continua en el intervalo cerrado [una B].
F es derivable en el intervalo abierto (una B).
F(la) = F(b).
Entonces hay un número c en (una B) Tal que F '(c) = 0.
El teorema del valor medio
Dejar F ser una función que satisface las siguientes hipótesis:
F es continua en el intervalo cerrado [una B].
F es derivable en el intervalo abierto (una B).
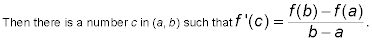
De Newton método de aproximación Fórmula
El método de Newton es una técnica que trata de encontrar una raíz de una ecuación. Para empezar, intenta elegir un número que es " cerca " al valor de una raíz y llamar a este valor X1. Recogiendo X1 puede implicar algo de ensayo y error- si usted está tratando con una función continua en un intervalo (o posiblemente toda la recta real), el teorema del valor intermedio puede reducir el intervalo considerado. Después de recoger X1, se utiliza la fórmula recursiva dada aquí para encontrar aproximaciones sucesivas:
Una palabra de precaución: Siempre verifique que su aproximación final es correcta (o cerca del valor de la raíz). El método de Newton puede fallar en algunos casos, en función del valor elegido para X1. Cualquier texto de cálculo que cubre el método de Newton debe señalar estas deficiencias.
El teorema fundamental del cálculo
Suponer F es continua en [una B]. Entonces las siguientes afirmaciones son ciertas:
La regla del trapezoide
dónde
Regla de Simpson
dónde n y es aún
Fórmulas especiales Límite de Cálculo
Fórmulas Derivados y de integración para funciones hiperbólicas
Las funciones hiperbólicas son ciertas combinaciones de las funciones exponenciales eX y e-X. Estas funciones se producen con bastante frecuencia en las ecuaciones diferenciales y de ingeniería que están normalmente introducen en un curso de Cálculo. Algunas de las aplicaciones de la vida real de estas funciones se relacionan con el estudio de los cables de transmisión y suspensión eléctricos.






