Cómo utilizar límites para determinar la continuidad

Aquí usted aprenderá acerca de la continuidad para un poco, a continuación, pasar a la conexión entre la continuidad y límites, y, finalmente, pasar a la definición formal de continuidad.

Definición El sentido común de la continuidad

La continuidad es un concepto tan simple - realmente. LA continuo función es simplemente una función sin espacios - una función que se puede dibujar sin tomar su lápiz en el papel. Considere las cuatro funciones de esta figura.

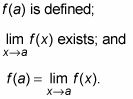
Sea o no una función es continua es casi siempre evidente. Las dos primeras funciones de esta figura - F (X) Y g(X) - No tienen lagunas, por lo que son continuas. Los dos siguientes - p(X) Y q(X) - Tienen lagunas en X = 3, así que no son continuas.

¡Eso es todo al respecto! Bueno, no del todo. Las dos funciones con lagunas no son continuas en todas partes, sino porque se puede dibujar secciones de ellos sin tomar su lápiz del papel, se puede decir que partes de esas funciones son continuas.

Y a veces, una función es continua en todas partes se define. Tal función se describe como continua en toda su dominio, lo que significa que su brecha o brechas ocurren en X-valores, donde no está definida la función. La funcion p(X) Es continua en toda su dominio- q(X), Por otro lado, no es continuo en toda su dominio porque no es continua en X = 3, que es en el dominio de la función. A menudo, la cuestión importante es si una función es continua en un particular, X-valor. Es a menos que haya un hueco allí.

Todas las funciones polinómicas son continuas en todas partes. Todas las funciones racionales - una función racional es el cociente de dos funciones polinómicas - son continuas sobre la totalidad de sus dominios.

La conexión continuidad límite

Con una gran excepción (que usted conseguirá en un minuto), la continuidad y los límites van de la mano. Por ejemplo, consideremos de nuevo las funciones F, g, p, y q. Funciones F y g son continuas en X = 3, y ambos tienen límites en X = 3. Funciones p y q, Por otro lado, no son continuas en X = 3, y no tienen límites en X = 3. La excepción a la regla se refiere a las funciones con agujeros. En realidad, cuando se llega a fin de cuentas, la excepción es más importante que la regla. Considere las dos funciones en la siguiente figura.

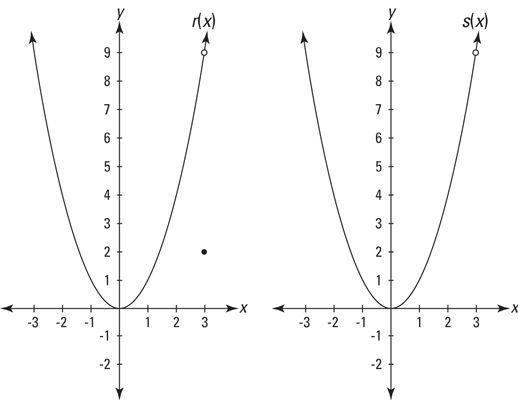
Estas funciones tienen deficiencias en X = 3 y, obviamente, no son continuos, pero sí tienen límites en cuanto X enfoques 3. En cada caso, el límite es igual a la altura del agujero. Un agujero infinitesimal en una función es el único lugar de una función puede tener un límite en el que no es continua.

Ambas funciones en la figura tienen el mismo límite X 3- aproxima el límite es de 9, y los hechos que r(3) = 2 y que s(3) no está definido son irrelevantes. Para ambas funciones, como X ceros en el 3 de cada lado, la altura de la función en los ceros de la altura del agujero - que es el límite.

El límite en un agujero es el colmo de un agujero.

Definición formal de continuidad

Una función F (X) Es continua en un punto X = la si las tres condiciones siguientes se cumplen:

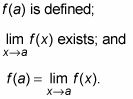
Al igual que con la definición formal de un límite, la definición de continuidad siempre se presenta como una prueba de 3 partes, pero la condición 3 es el único que usted necesita preocuparse porque 1 y 2 se incorporan a 3. Usted debe recordar, sin embargo , que la condición 3 es no satisfecho cuando los lados izquierdo y derecho de la ecuación son tanto indefinido o inexistente.