Cómo identificar pares y funciones impares y sus gráficas
Saber si una función es par o impar ayuda a graficar porque esa información le indica que la mitad de los puntos que usted tiene para graficar. Estos tipos de funciones son simétricas, por lo que lo que está en un lado es exactamente el mismo que el otro lado. Si una función es par, la gráfica es simétrica con respecto al y-eje. Si la función es impar, la gráfica es simétrica con respecto al origen.
Incluso funcionar: La definición matemática de una incluso la función es F(-X) = F(X) Para cualquier valor de X. El ejemplo más sencillo de esto es F(X) = X2 porque f (x) = f (-x) para todos X. Por ejemplo, F(3) = 9, y F(-3) = 9. Básicamente, la entrada opuesta produce la misma salida.
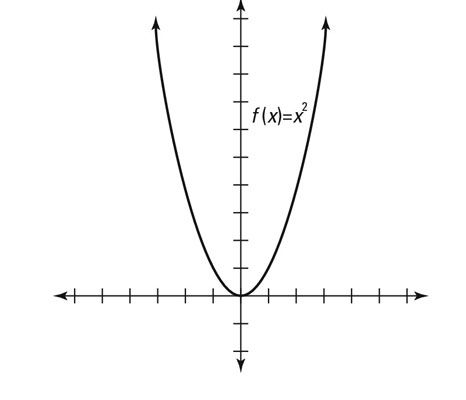
Visualmente hablando, la gráfica es una imagen especular acerca de la y-eje, como se muestra aquí.
Función impar: La definición de un función impar es F(-X) = -F(X) Para cualquier valor de X. La entrada opuesta da la salida opuesta. Estos gráficos tienen simetría 180 grados alrededor del origen. Si activa la gráfica al revés, se ve igual.
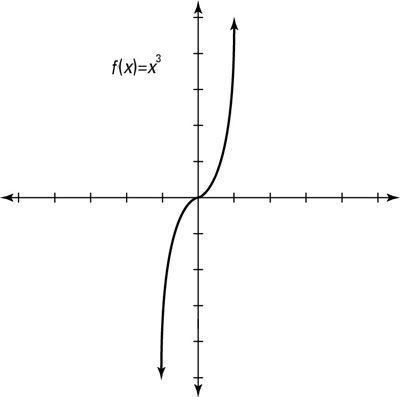
El ejemplo que se muestra aquí, F(X) = X3, es una función impar, porque f (-x) = - f (x) para todos X. Por ejemplo, F(3) = 27 y F(-3) = -27.
Cómo graficar y transformar una función exponencial Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…
Cómo graficar una función seno Sabiendo cómo graficar funciones trigonométricas le permite medir el movimiento de los objetos que se mueven hacia atrás y hacia adelante o hacia arriba y hacia abajo en un intervalo regular, como péndulos. Funciones seno son formas perfectas de…
Cómo graficar funciones con más de una regla: funciones a nivel de pieza Funciones con más de una regla (llamados pfunciones IECE-sabios) Se rompen en pedazos, dependiendo de la entrada. Aunque una función a nivel de pieza tiene más de una función, cada función está definida sólo en un intervalo específico.…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
Cómo interpretar las gráficas de funciones Vas a ver a decenas y decenas de funciones en su estudio del cálculo, y las gráficas de estas funciones puede expresar visualmente las cosas tales como la inflación, el crecimiento demográfico y la desintegración radiactiva. A continuación se…
Cómo reflejar la gráfica de una función Reflexiones tomar una función madre y proporcionar una imagen especular de la vuelta, ya sea una línea horizontal o vertical. Te encontrarás con dos tipos de reflexiones:Un número negativo se multiplica toda la función La negativa fuera de la…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Encuentre la imagen especular de una función de la trigonometría en un gráfico Cuando multiplicas una función trigonométrica de un número negativo, todos los valores de salida se invierten en la señal. Los valores positivos se vuelven negativos y los valores negativos se convierten en positivos. El efecto que esta…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Graficar las asíntotas de una función cotangente Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.Las gráficas de estas dos funciones son…