3 Principales modelo de probabilidad lineal (lpm) problemas

Utilizando la técnica de mínimos cuadrados ordinarios (OLS) para estimar un modelo con una variable dependiente maniquí se conoce como la creación de un modelo de probabilidad lineal,

o LPM. LPMs no son perfectos. Pueden surgir tres problemas específicos:

• No normalidad del término de error

• Errores heterocedástica

• Potencialmente predicciones absurdas

No normalidad del término de error

La suposición de que se distribuye normalmente el error es fundamental para la realización de pruebas de hipótesis después de estimar el modelo econométrico.

El término de error de un LPM tiene una distribución binomial en lugar de una distribución normal. Esto implica que el tradicional t-pruebas de significación individual y F-pruebas de significación global no son válidos.

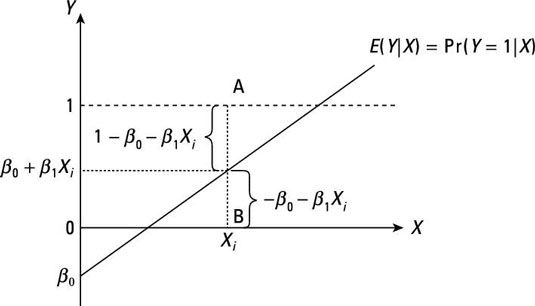
Como se puede ver, el término de error en un LPM tiene uno de dos valores posibles para un determinado X valor. Un valor posible para el error (si Y = 1) viene dada por A, y el otro valor posible para el error (si Y = 0) está dada por B. En consecuencia, es imposible que el término de error de tener una distribución normal.

Heterocedasticidad

El modelo de regresión lineal clásico (CLRM) supone que el término de error es homocedástico. Se requiere que el supuesto de homocedasticidad para demostrar que los estimadores MCO son eficientes (o mejor). La prueba de que los estimadores MCO son eficientes es un componente importante del teorema de Gauss-Markov. La presencia de heterocedasticidad puede hacer que el teorema de Gauss-Markov a ser violada y dar lugar a otras características indeseables para los estimadores MCO.

El término de error en un LPM es heterocedástica porque la varianza no es constante. En lugar de ello, la varianza de un término de error LPM depende del valor de la variable independiente (s).

Usando la estructura de la LPM, se puede caracterizar la varianza de su término de error de la siguiente

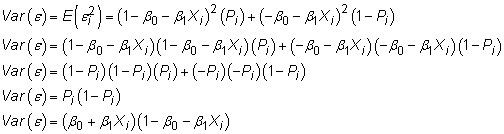
Debido a que la varianza del error depende del valor de X, exhibe heteroscedasticidad en lugar de homocedasticidad.

Probabilidades predichas no acotadas

La ley más básica de probabilidad indica que la probabilidad de que ocurra un evento debe estar contenido en el intervalo [0,1]. Pero la naturaleza de un LPM es tal que no garantiza esta ley fundamental de la probabilidad es satisfecho. Aunque la mayoría de las probabilidades predichas de un LPM tienen valores razonables (entre 0 y 1), algunas probabilidades predichas pueden tener valores sin sentido que son menos que 0 o mayor que 1.

Echa un vistazo a la siguiente figura y centrar su atención en los segmentos de la línea de regresión, donde la probabilidad condicional es mayor que 1 o menor que 0. Cuando la variable dependiente es continua, usted no tiene que preocuparse acerca de los valores sin límites para el medios condicionales. Sin embargo, las variables dicotómicas son problemáticos porque los medios condicionales representan probabilidades condicionales. Interpretación de probabilidades que no están limitadas por 0 y 1 es difícil.

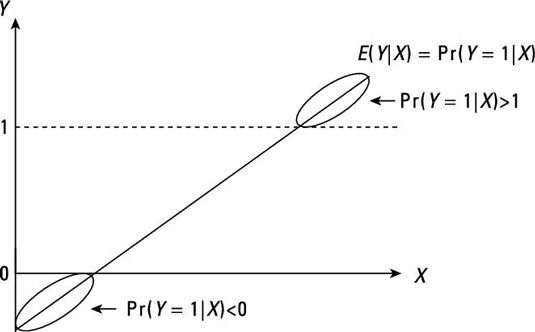
Se puede ver un ejemplo de este problema con los datos reales:

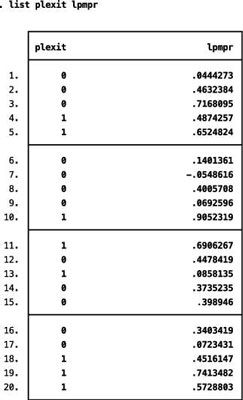
La mayor parte de las probabilidades estimadas de la estimación LPM están contenidos dentro del intervalo [0,1], pero la probabilidad predicha por séptima observación es negativo. Por desgracia, no hay nada en la estimación de un LPM asegura que todas las probabilidades predichas se mantengan dentro de los valores razonables.