¿Cómo distinguir entre perturbaciones homocedástico y heteroscedásticos

El término de error es el componente más importante del modelo de regresión lineal clásica (CLRM). La mayor parte de los supuestos que permiten econometristas CLRM para probar las propiedades deseables de los estimadores MCO (el teorema de Gauss-Markov) implican directamente características sobre el término de error (o perturbaciones). Uno de los supuestos CLRM se ocupa de la varianza condicional del término- error a saber, que la varianza del término de error es constante (homocedástico).

Error homocedástico frente error heterocedástica

CLRM se basa en el término de error varianza es constante. Introduce el término homocedasticidad, el cual se refiere a una situación en la que el error tiene la misma varianza independientemente del valor (s) adoptada por la variable independiente (s). Los econometristas suelen expresar homocedasticidad como

dónde X_yo representa un vector de valores para cada individuo y para todas las variables independientes.

Como puede ver, cuando el término de error es homocedástico, la dispersión del error sigue siendo el mismo en todo el rango de observaciones e independientemente de forma funcional.

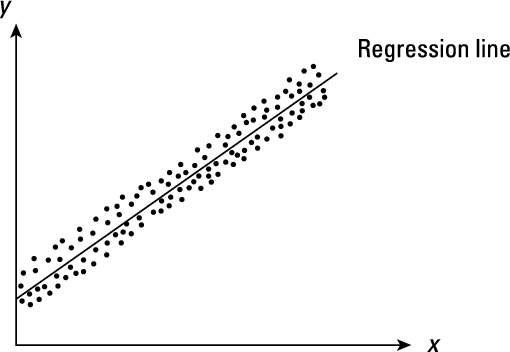
En muchas situaciones, el término de error no tiene una varianza constante, dando lugar a élteroskedasticity - cuando la varianza de los cambios término de error en respuesta a un cambio en el valor (s) de la variable independiente (s). Los econometristas suelen expresar heteroscedasticidad como

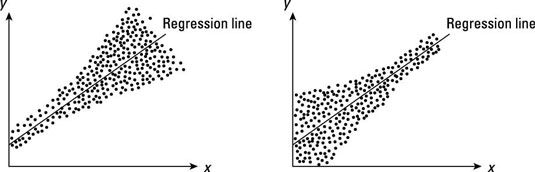
Si el término de error es heterocedástica, la dispersión del error cambia en el rango de observaciones, como se muestra. Los patrones de heterocedasticidad representados son sólo un par entre muchos patrones posibles. Cualquier variación de error que no se parece que en la figura anterior es probable que sea heterocedástica.

Si usted recuerda que homogéneo significa uniforme o idénticos, mientras que heterogenea se define como una variedad o diferentes, usted puede tener un tiempo más fácil recordar el concepto de heteroscedasticidad siempre. ¡Eres afortunado!

Las consecuencias de heteroscedasticidad

Heterocedasticidad viola uno de los supuestos CLRM. Cuando se viola el supuesto del CLRM, los estimadores MCO pueden ya no ser azul (mejores estimadores lineales insesgados).

En concreto, en la presencia de heteroscedasticidad, los estimadores MCO pueden no ser eficiente (conseguir la varianza más pequeña). Además, los errores estándar estimados de los coeficientes serán sesgados, lo que resulta en pruebas de hipótesis poco fiables (t-estadísticas). Las estimaciones de MCO, sin embargo, siguen siendo imparcial.

Bajo el supuesto de homocedasticidad, en un modelo con una variable independiente

la varianza del coeficiente de la pendiente estimada es

dónde

es la varianza del error homocedástico y

Sin embargo, sin el supuesto de homocedasticidad, la varianza de

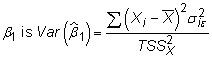
dónde

es la varianza heterocedástica del error.

Por lo tanto, si usted no puede explicar adecuadamente para heteroscedasticidad en su presencia, inadecuadamente calcular las desviaciones y los errores estándar de los coeficientes. los t-estadística para los coeficientes se calcula con

Por lo tanto, cualquier sesgo en el cálculo de los errores estándar se transmite a su t-estadísticas y conclusiones sobre la significación estadística.

Heterocedasticidad es un problema común para la estimación de regresión OLS, especialmente con datos de corte transversal y de panel. Sin embargo, por lo general, no tiene manera de saber de antemano si va a estar presente, y la teoría rara vez es útil para anticipar su presencia.