Cómo seleccionar variables independientes para su modelo econométrico
Una de las decisiones más importantes que hacer cuando se especifica el modelo econométrico es que las variables a incluir como variables independientes. Aquí, se entera de lo que pueden producirse problemas si incluye muy pocas o demasiadas variables independientes en el modelo, y ves cómo esta mala especificación afecta a los resultados.
La omisión de variables relevantes
Si una variable que pertenece en el modelo se excluye de la función de regresión estimado, el modelo está mal y puede causar sesgo en los coeficientes estimados.
Usted tiene un sesgo variable omitida si una variable excluida tiene algún efecto (positivo o negativo) en su variable dependiente y está correlacionada con al menos una de las variables independientes.
La naturaleza matemática de sesgo de especificación se puede expresar usando un modelo simple. Supongamos que el verdadero modelo de población está dada por
dónde X1 y X2 son las dos variables que afectan Y. Pero debido a la ignorancia o la falta de datos, en lugar a estimar esta regresión:
que omite X2 a partir de las variables independientes. El valor esperado de
en esta situación es
Pero esta ecuación viola el teorema de Gauss-Markov porque
La magnitud del sesgo se puede expresar como
dónde
si el efecto de X2 en Y y
es la pendiente de esta regresión:
que captura la correlación (positiva o negativa) entre la variable (s) incluidos y excluidos.
| Impacto de la variable omitida en la Variable Dependiente | Correlación entre incluidos y omite variable: | |
|---|---|---|
| Positivo | Negativo | |
| Positivo | Sesgo positivo | Sesgo negativo |
| Negativo | Sesgo negativo | Sesgo positivo |
En la práctica, es muy probable que tener algún sesgo de la variable omitida porque es imposible de controlar por todo lo que afecta a la variable dependiente. Sin embargo, puede aumentar las posibilidades de reducir al mínimo sesgo de variables omitidas, evitando modelos de regresión simple (con una variable independiente) y que incluye las variables que pueden ser los más importantes en teoría (y, posiblemente, pero no necesariamente estadísticamente) en la explicación de la variable dependiente .
Incluyendo variables irrelevantes
Si una variable no tiene cabida en el modelo y se incluye en la función de regresión estimada, el modelo se falte espacio. Si overspecify el modelo de regresión mediante la inclusión de una variable irrelevante, los coeficientes estimados siguen siendo imparcial. Sin embargo, tiene un efecto no deseable de aumentar los errores estándar de sus coeficientes.
En un modelo de regresión simple (con una variable independiente), el error estándar estimado del coeficiente de regresión para X es
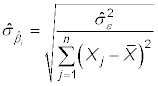
dónde
es la varianza estimada del error y
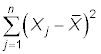
es la variación total en X.
Si incluye variables independientes adicionales en el modelo, el error estándar estimado para cualquier coeficiente de regresión dada está dada por
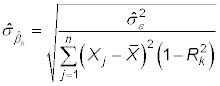
dónde
es R-cuadrado de la regresión de la Xk en las demás variables independientes o Xs. Porque
el numerador disminuye. Una variable irrelevante no ayuda a explicar alguna de la variación en Y, así que sin una disminución en la compensación
los aumentos de error estándar.
Sólo porque su coeficiente estimado no es estadísticamente significativa no significa que sea irrelevante. Un modelo bien especificado suele incluir algunas variables que son estadísticamente significativos y algunos que no lo son. Además, las variables que no son estadísticamente significativas puede contribuir bastante variación explicada a tener ningún impacto negativo en los errores estándar.




