Econometría y el modelo log-lineal
Si utiliza valores logarítmicos naturales para su variable dependiente (Y) Y mantener sus variables independientes (X) En su escala original, la especificación econométrica se llama log-lineal del modelo. Estos modelos se utilizan normalmente cuando usted piensa las variables pueden tener una relación de crecimiento exponencial.
Por ejemplo, si pones un poco de dinero en una cuenta de ahorro, que espera ver el efecto del interés compuesto con un crecimiento exponencial de su dinero! El modelo original en estos tipos de escenarios no es lineal en los parámetros, pero una transformación logarítmica genera la linealidad deseada.
Considere el siguiente modelo de valor en un fondo de ahorro que depende de su inversión inicial, su rentabilidad, y la longitud de tiempo en que los fondos se invierten: Yt = Y0(1 + r)t, dónde Yt representa el valor del fondo en el momento t, Y0 es la inversión inicial en el fondo de ahorro, y r es la tasa de crecimiento.
Economistas laborales también están interesados en funciones similares porque las personas suelen tener algún poder adquisitivo inicial que puede ser complementado con inversiones en la adquisición de habilidades. Estas hufunciones de capitales hombre hacer frente a la cantidad de dinero que una persona puede llegar a ganar en función de sus capacidades y de las inversiones iniciales en la educación, formación, experiencia, y así sucesivamente.
Una función de crecimiento exponencial genérica se puede escribir como Y = Y0(1 + r)X, donde el valor de Y para una determinada X se puede derivar sólo si la tasa de crecimiento (r) es sabido. La tasa de crecimiento puede ser estimado, pero una transformación logarítmica debe ser utilizado para estimar usando OLS.
Si usted comienza con un modelo de crecimiento exponencial y tomar el logaritmo de ambos lados, usted termina con ln Y = ln Y0 + Xln (1 + r), dónde ln Y0 es la constante desconocida y ln (1 + r) Es la tasa de crecimiento desconocido más 1 (en forma de logaritmo natural). Se termina con el siguiente modelo:
Se puede estimar este modelo con OLS simplemente usando los valores de registro naturales para la variable dependiente (Y) Y la escala original para las variables independientes (X). Es conocido como log-lineal del modelo.
Después de estimar un modelo log-lineal, los coeficientes se pueden utilizar para determinar el impacto de las variables independientes (X) Sobre la variable dependiente (Y). Los coeficientes en un modelo log-lineal representan la prevista cambio porcentual en la variable dependiente para un cambio de unidad en la variable independiente. El coeficiente
proporciona el instantanetasa ous del crecimiento.
Usando el cálculo con un modelo log-lineal simple, se puede mostrar cómo se deben interpretar los coeficientes. Comience con el modelo
y diferenciarlo para obtener
El término de la derecha;-lado es la unidad de cambio en X, y el término de la izquierda;-lado es el porcentaje de cambio en Y, así
proporciona el yontasa de crecimiento de stantaneous para Y asociado con un cambio unitario en X.
los tasa de crecimiento compuesto se considera que es una estimación más precisa del impacto de X. Después de estimar un modelo log-lineal, se puede calcular la tasa de crecimiento compuesto (r) Como
Supongamos que usted obtiene la regresión estimada
dónde Y es el salario de un individuo y X es sus años de educación. El valor de 0,08
indica que el retorno instantáneo para un año adicional de educación es del 8 por ciento y el retorno compuesto es de 8.3 por ciento (e0.08 - 1 = 0,083).
Si usted estima una regresión log-lineal, un par de resultados para el coeficiente de X producir los más probables relaciones:
Esta función log-lineal muestra un impacto positivo de la variable independiente, como se muestra en la parte (a).
Esta función log-lineal representa un impacto negativo de la variable independiente, como se muestra en la parte (b).
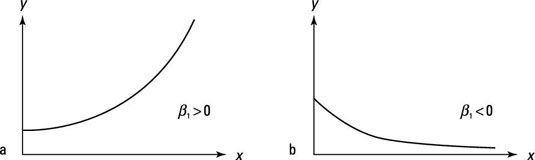
Los coeficientes de regresión en un modelo log-lineal no representan la pendiente.
Cómo estimar los efectos de estacionalidad Efectos de estacionalidad se pueden correlacionar con las dos variables dependientes e independientes. A fin de evitar confundir los efectos de estacionalidad con los de las variables independientes, es necesario controlar de forma explícita para…
Cómo seleccionar variables independientes para su modelo econométrico Una de las decisiones más importantes que hacer cuando se especifica el modelo econométrico es que las variables a incluir como variables independientes. Aquí, se entera de lo que pueden producirse problemas si incluye muy pocas o demasiadas…
Cómo configurar la función de regresión poblacional modelo (PRF) Antes de comenzar con el análisis de regresión, es necesario identificar el regre poblaciónsfunción sión (PRF). El PRF define la realidad (o su percepción de ella) en su relación con su tema de interés. Para identificarlo, es necesario…
Multicolinealidad perfecta y el modelo econométrico Conseguir un asimiento en multicolinealidad perfecta, que es poco frecuente, es más fácil si se puede imaginar un modelo econométrico que utiliza dos variables independientes, tales como las siguientes:Supongamos que, en este modelo,donde los…
Proyección de tendencias temporales con oles La mayoría de las series de tiempo económicas crecen con el tiempo, pero a veces las series temporales en realidad disminuyen con el tiempo. En cualquier caso, usted está buscando en una tendencia en el tiempo. Los modelos más comunes captura de…
Funciones cuadráticas ofrecen flexibilidad en la econometría Dado que las relaciones económicas son raramente lineal, es posible que desee permitir que su modelo econométrico para tener cierta flexibilidad. Con una función cuadrática, usted permite que el efecto de la variable independiente (X) Sobre la…
Especificar el modelo de regresión de la econometría En la econometría, el modelo de regresión es un punto de partida común de un análisis. A medida que define el modelo de regresión, es necesario tener en cuenta varios elementos:La teoría económica, la intuición y el sentido común deben todo…
Especificación de funciones no lineales apropiadas: los modelos probit y logit Si el resultado de interés es cualitativa, se utiliza una variable dependiente maniquí y estimar la probabilidad de que el resultado (Y = 1) se produce utilizando el modelo econométrico. Aunque OLS se pueden utilizar para estimar un modelo con…
Los 2 tipos de multicolinealidad Multicollinearity surge cuando existe una relación lineal entre dos o más variables independientes en un modelo de regresión. En la práctica, rara vez se encuentra con multicolinealidad perfecta, pero de alta multicolinealidad es bastante común…
Trabajar con variables dependientes especiales en la econometría Muchos fenómenos económicos son dicotómicas en naturaleza- en otras palabras, el resultado ya sea se produce o no se produce. Los resultados dicotómicos son el tipo más común de variables dependientes discretas o cualitativas analizadas en…
Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y la dirección de la relación entre dos o más variables. El…
Cómo estimar una tendencia en un modelo de regresión de series de tiempo Para estimar un modelo de regresión de series de tiempo, una tendencia debe ser estimado. Se empieza por la creación de un gráfico de líneas de las series temporales. El gráfico de líneas muestra cómo una variable cambia con el tiempo- que…