Econometría y el modelo log-log

Utilizando logaritmos naturales para las variables en ambos lados de su especificación econométrica se llama log-log modelo. Este modelo es útil cuando la relación no es lineal en los parámetros, ya que la transformación logarítmica genera la linealidad deseada en los parámetros (se recordará que la linealidad en los parámetros es uno de los supuestos MCO).

En principio, cualquier transformación logarítmica (o natural no) se puede utilizar para transformar un modelo que es no lineal en los parámetros en uno lineal. Todas las transformaciones de registro generan resultados similares, pero la convención en el trabajo econométrico aplicado es utilizar el logaritmo natural. La ventaja práctica del logaritmo natural es que la interpretación de los coeficientes de regresión es sencillo.

Considere la función de demanda

dónde Q es la cantidad demandada, alfa es un parámetro de desplazamiento, P es el precio del bien, y la beta parámetro es menor que cero para una curva de demanda con pendiente descendente.

usted puede reconocer la función como un tipo específico de la curva de demanda con elasticidad igual a -1 en absoluto puntos- que es, tiene una curva de demanda elástica unitaria.

Una curva de demanda de la forma

tiene una elasticidad constante, pero el valor de la elasticidad que puede no ser conocida. Utilizando los datos, se puede estimar los parámetros, pero debe transformar la función con el fin de realizar estimaciones utilizando la técnica OLS.

Si su modelo no es lineal en los parámetros, a veces una transformación logarítmica logra linealidad.

Una forma genérica de un modelo de elasticidad constante puede ser representado por

Si se toma el logaritmo natural de ambos lados, usted termina con

Tratas

como el intercepto. Se termina con el siguiente modelo:

Se puede estimar este modelo con OLS simplemente usando los valores de registro natural para las variables en lugar de su escala original.

Después de estimar un modelo log-log, como el que en este ejemplo, los coeficientes pueden utilizarse para determinar el impacto de las variables independientes (X) Sobre la variable dependiente (Y). Los coeficientes en un modelo log-log representan la elasticidad de tu Y variable con respecto a su X variable. En otras palabras, el coeficiente es la prevista cambio porcentual en la variable dependiente para un cambio porcentual en la variable independiente.

Usando el cálculo con un modelo log-log simple, usted puede mostrar cómo se deben interpretar los coeficientes. Comience con el modelo

y diferenciarlo para obtener

El término de la derecha; lado es el porcentaje de cambio en X, y el término de la izquierda; lado es el porcentaje de cambio en Y, así

mide la elasticidad.

Supongamos que usted obtenga las estimaciones

dónde Y es ventas y X es el precio. La elasticidad es -0.85, por lo que un aumento del 1 por ciento en el precio se asocia con una disminución de 0,85 por ciento en la cantidad demandada (ventas), en promedio.

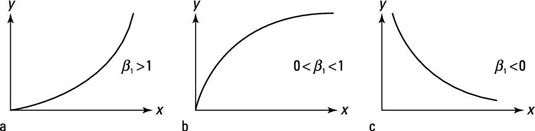
Si usted estima una regresión log-log, unos resultados para el coeficiente de X producir los más probables relaciones:

La parte (a) muestra esta función log-log en el que el impacto de la variable independiente es positiva y se hace más grande que su valor aumenta.

La parte (b) muestra una función log-log en el que el impacto de la variable independiente es positivo, pero se hace más pequeño que su valor aumenta.

Parte (c) muestra una función log-log, donde el impacto de la variable dependiente es negativo.

Aunque los coeficientes de regresión se denominan a veces coeficientes de pendiente parcial, en un modelo log-log de los coeficientes no representan la pendiente (o unidad de cambio en su Y variable para un cambio unitario en su X variable).