Alta multicolinealidad y el modelo econométrico

Resultados de alta multicolinealidad de una relación lineal entre las variables independientes con un alto grado de correlación, pero no son completamente determinista (en otras palabras, que no tienen correlación perfecta). Es mucho más común de lo que su contraparte perfecta y puede ser igualmente problemático cuando se trata de estimar un modelo econométrico.

Se puede describir una relación lineal aproximada, que caracteriza alta multicolinealidad, como sigue:

donde el Xs son variables independientes en un modelo de regresión y u representa un término de error aleatorio (que es el componente que diferencia alta multicolinealidad de multicolinealidad perfecta). Por lo tanto, la diferencia entre multicolinealidad perfecta y alta es que alguna variación en la variable independiente no se explica por la variación en la otra variable independiente (s).

Cuanto más fuerte es la relación entre las variables independientes, más probable es que tenga problemas de estimación con su modelo.

Relaciones lineales fuertes que resulta en alta multicolinealidad veces se puede coger por sorpresa, pero estas tres situaciones tienden a ser especialmente problemático:

• Utiliza las variables que son los valores de los otros rezagados. Por ejemplo, una variable independiente es el ingreso de un individuo en el año en curso, y otro variable independiente mide los ingresos de un individuo en el año anterior. Estos valores pueden ser completamente diferente para algunas observaciones, pero para la mayoría de las observaciones que los dos están estrechamente relacionados.

• Utiliza las variables que comparten un componente común tendencia temporal. Por ejemplo, utiliza valores anuales para el PIB (producto interno bruto) y el Dow Jones (Dow Jones Industrial Average) como variables independientes en un modelo de regresión. El valor para estas mediciones tiende a aumentar (con disminuciones ocasionales) y generalmente se mueven en la misma dirección con el tiempo.

• Utiliza las variables que capturan fenómenos similares. Por ejemplo, las variables independientes para explicar la delincuencia en las ciudades pueden ser las tasas de desempleo, los ingresos medios, y los índices de pobreza. Estas variables no son susceptibles de ser perfectamente correlacionados, pero probablemente son altamente correlacionados.

Técnicamente, la presencia de alta multicolinealidad no viola ninguna hipótesis CLRM. En consecuencia, las estimaciones de MCO se pueden obtener y son de color azul (mejores estimadores lineales insesgados) con una alta multicolinealidad.

Aunque estimadores MCO permanecen AZUL en presencia de alta multicolinealidad, refuerza una deseable muestreo repetido propiedad. En la práctica, es probable que no tienen la oportunidad de utilizar múltiples muestras, por lo que desea cualquier muestra dada para producir resultados sensibles y fiables.

Con alta multicolinealidad, el OLS estimaciones todavía tienen la varianza más pequeña, pero más pequeño es un concepto relativo y no garantiza que las varianzas son realmente pequeñas. De hecho, las variaciones más grandes (y los errores estándar) de los estimadores MCO son la razón principal para evitar alta multicolinealidad.

Las consecuencias típicas de alta multicolinealidad incluyen los siguientes:

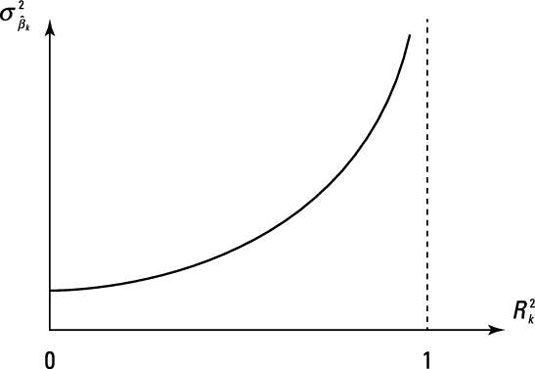
• Errores estándar más grandes y insignificante t-estadísticas: La varianza estimada de un coeficiente en una regresión múltiple es

  

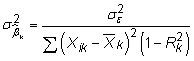
  dónde

  

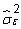
  es el error cuadrático medio (MSE) y

  

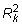
  es el valor R-cuadrado de la regresión X_k en el otro Xs. Mayores resultados multicolinealidad en una más grande

  

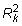
  lo que aumenta el error estándar del coeficiente. La figura ilustra el efecto de multicolinealidad en la varianza (o error estándar) de un coeficiente.

  

  Porque el t-estadística asociada con un coeficiente es la relación entre el coeficiente estimado para el error estándar

  

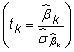
  alta multicolinealidad también tiende a dar como resultado insignificante t-estadísticas.

• Estimaciones de los coeficientes que son sensibles a los cambios en la especificación: Si las variables independientes son altamente alineados, las estimaciones deben enfatizan pequeñas diferencias en las variables con el fin de asignar un efecto independiente de cada uno de ellos. Adición o eliminación de las variables del modelo se puede cambiar la naturaleza de las pequeñas diferencias y cambiar drásticamente sus estimaciones de los coeficientes. En otras palabras, sus resultados no son robustos.

• Signos de los coeficientes sin sentido y magnitudes: Con más alta multicolinealidad, la varianza de los coeficientes estimados se incrementa, lo que a su vez aumenta las posibilidades de obtener estimaciones de los coeficientes con los valores extremos. En consecuencia, estas estimaciones pueden tener increíblemente grandes magnitudes y / o signos que contrarresten la relación esperada entre las variables independientes y dependientes. La figura ilustra cómo la distribución muestral de los coeficientes estimados se ve afectada por la multicolinealidad.

  

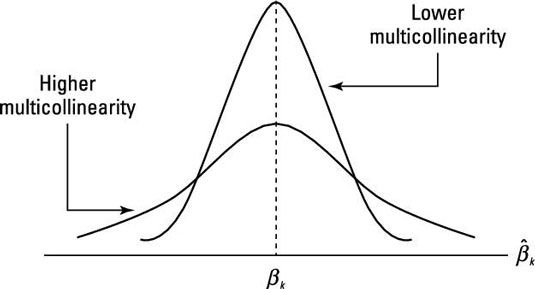
Cuando dos (o más) variables que muestran una alta multicolinealidad, hay más incertidumbre en cuanto a qué variable debe ser acreditado con la explicación de la variación en la variable dependiente. Por esta razón, un alto R-valor al cuadrado combinado con muchos coeficientes estadísticamente insignificantes es una consecuencia común de alta multicolinealidad.