Multicolinealidad perfecta y el modelo econométrico
Conseguir un asimiento en multicolinealidad perfecta, que es poco frecuente, es más fácil si se puede imaginar un modelo econométrico que utiliza dos variables independientes, tales como las siguientes:
Supongamos que, en este modelo,
donde los alfas son constantes. Por sustitución, se obtiene
lo que indica que el modelo se derrumba y no se puede estimar como se especifica originalmente.
Multicolinealidad perfecta ocurre cuando dos o más variables independientes en un modelo de regresión muestran una determinista (perfectamente predecible o que no contiene aleatoriedad) relación lineal.
El resultado de multicolinealidad perfecta es que no se puede obtener cualquier inferencias estructurales sobre el modelo original utilizando datos de la muestra para la estimación. En un modelo con multicolinealidad perfecta, sus coeficientes de regresión son indeterminados y sus errores estándar son infinitas.
Multicolinealidad perfecta por lo general ocurre cuando los datos se ha construido o manipulada por el investigador. Por ejemplo, usted tiene multicolinealidad perfecta si se incluye una variable dummy para cada grupo posible o categoría de una característica cualitativa en lugar de incluir una variable para todos menos uno de los grupos.
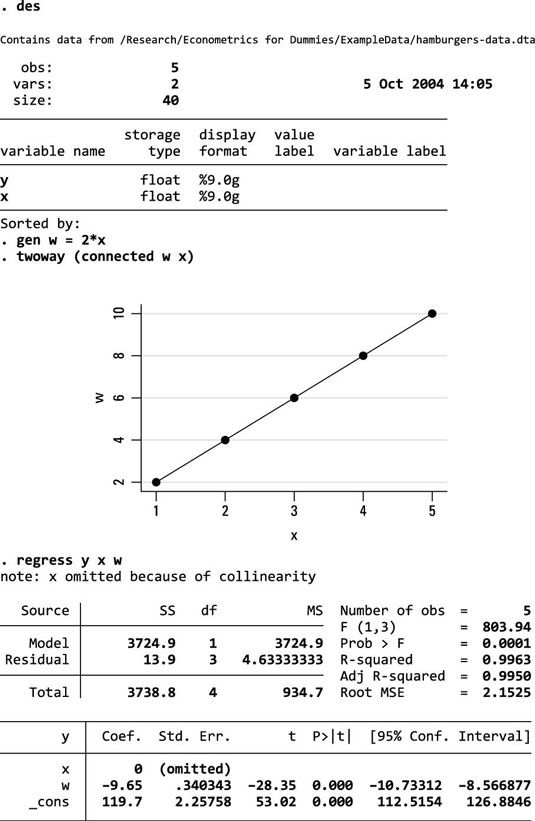
En la siguiente figura, STATA se utiliza para crear una variable que es una combinación lineal de otra variable. Entonces la gráfica de las dos variables se representa e incluye tanto de ellos como variables independientes en un modelo de regresión. Nótese, sin embargo, que los resultados no contienen estimaciones de los parámetros para ambas variables. La obtención de los coeficientes de regresión individuales para cada variable es imposible si usted tiene multicolinealidad perfecta.
La mayoría de los programas de software econométricos identifican multicolinealidad perfecta y soltar uno (o más) las variables antes de proporcionar los resultados de las estimaciones, atendiendo el problema para usted. La buena noticia es que se puede evitar la multicolinealidad perfecta, al mostrar un poco de cuidado en la creación de las variables y cuidadosamente elegir cuáles incluyen como variables independientes.
-
Cómo utilizar regresiones lineales en el análisis predictivo - 10 Componentes de un buen proyecto de investigación econometría
- Estimación econométrica y los supuestos CLRM
- Econometría: elección de la forma funcional de su modelo de regresión
-
Econometría y el modelo log-lineal -
Econometría para los maniquíes
Econometría y el modelo log-log Utilizando logaritmos naturales para las variables en ambos lados de su especificación econométrica se llama log-log modelo. Este modelo es útil cuando la relación no es lineal en los parámetros, ya que la transformación logarítmica genera la…
La estimación de la función de regresión y de los residuos La función de regresión se suele expresar matemáticamente en una de las siguientes maneras: notación básica, notación sumatoria o notación matricial. los Y variable representa el resultado que le interesa, llamada la variable dependiente, y…
Alta multicolinealidad y el modelo econométrico Resultados de alta multicolinealidad de una relación lineal entre las variables independientes con un alto grado de correlación, pero no son completamente determinista (en otras palabras, que no tienen correlación perfecta). Es mucho más común…
Cómo desestacionalizar los datos de series de tiempo En muchos casos, los patrones estacionales se quitan de los datos de series de tiempo cuando están en libertad bajo las bases de datos públicas. Los datos que han sido despojados de sus patrones estacionales se conoce como seasonally ajustada o…
Cómo estimar los efectos de estacionalidad Efectos de estacionalidad se pueden correlacionar con las dos variables dependientes e independientes. A fin de evitar confundir los efectos de estacionalidad con los de las variables independientes, es necesario controlar de forma explícita para…
¿Cómo encontrar diferencias promedio utilizando una variable ficticia Usted debe recordar de su curso de estadística cómo llevar a cabo la t-prueba para examinar las diferencias de medias entre dos grupos. Pero lo que no saben es que se puede utilizar variables ficticias y análisis de regresión para obtener los…
Cómo seleccionar variables independientes para su modelo econométrico Una de las decisiones más importantes que hacer cuando se especifica el modelo econométrico es que las variables a incluir como variables independientes. Aquí, se entera de lo que pueden producirse problemas si incluye muy pocas o demasiadas…
Cómo configurar la función de regresión poblacional modelo (PRF) Antes de comenzar con el análisis de regresión, es necesario identificar el regre poblaciónsfunción sión (PRF). El PRF define la realidad (o su percepción de ella) en su relación con su tema de interés. Para identificarlo, es necesario…
Especificar el modelo de regresión de la econometría En la econometría, el modelo de regresión es un punto de partida común de un análisis. A medida que define el modelo de regresión, es necesario tener en cuenta varios elementos:La teoría económica, la intuición y el sentido común deben todo…
Los 2 tipos de multicolinealidad Multicollinearity surge cuando existe una relación lineal entre dos o más variables independientes en un modelo de regresión. En la práctica, rara vez se encuentra con multicolinealidad perfecta, pero de alta multicolinealidad es bastante común…
Trabajar con variables dependientes especiales en la econometría Muchos fenómenos económicos son dicotómicas en naturaleza- en otras palabras, el resultado ya sea se produce o no se produce. Los resultados dicotómicos son el tipo más común de variables dependientes discretas o cualitativas analizadas en…
Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y la dirección de la relación entre dos o más variables. El…