Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones

El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y ​​la dirección de la relación entre dos o más variables. El analista puede utilizar el análisis de regresión para determinar la relación real entre estas variables examinado ventas y los beneficios de una empresa durante los últimos años. Los resultados de la regresión muestran si esta relación es válida.

Además de las ventas, otros factores también pueden determinar las ganancias de la corporación, o puede resultar que las ventas no explican las ganancias en absoluto. En particular, los investigadores, analistas, gestores de cartera y los comerciantes pueden utilizar el análisis de regresión para estimar las relaciones históricas entre los diferentes activos financieros. A continuación, puede utilizar esta información para desarrollar estrategias de negociación y medir el riesgo contenida en una cartera.

El análisis de regresión es una herramienta indispensable para el análisis de las relaciones entre las variables financieras. Por ejemplo, se puede:

• Identificar los factores que son más responsables de las ganancias de una empresa

• Determinar la cantidad de un cambio en las tasas de interés tendrá un impacto en una cartera de bonos

• Desarrollar una previsión del valor futuro del Promedio Industrial Dow Jones

Las diez secciones siguientes describen los pasos utilizados para implementar un modelo de regresión y analizar los resultados.

Paso 1: Especificar la variable dependiente e independiente (s)

Para poner en práctica un modelo de regresión, es importante especificar correctamente la relación entre las variables que se utiliza. El valor de una variable dependiente se supone que está relacionada con el valor de uno o más variables independientes. Por ejemplo, supongamos que un investigador está investigando los factores que determinan la tasa de inflación. Si el investigador cree que la tasa de inflación depende de la tasa de crecimiento de la oferta monetaria, se puede estimar un modelo de regresión utilizando la tasa de inflación como la variable dependiente y la tasa de crecimiento de la oferta monetaria como la variable independiente.

Un modelo de regresión basada en una única variable independiente se conoce como una sencillo modelo- de regresión con dos o más variables independientes, el modelo se conoce como una múltiple modelo de regresión.

Paso 2: Verificar la linealidad

Uno de los supuestos fundamentales de análisis de regresión es que la relación entre las variables dependientes e independientes es lineal (es decir, la relación se puede ilustrar con una linea recta.) Una de las maneras más rápidas para comprobar esto es para graficar las variables utilizando un gráfico de dispersión. Un diagrama de dispersión muestra la relación entre dos variables con la variable dependiente (Y) en el eje vertical y la variable independiente (X) en el eje horizontal.

Por ejemplo, supongamos que un analista cree que el exceso de rentabilidad a la Coca-Cola Stock dependen de los rendimientos superiores a la Standard and Poors (SP) 500. (El exceso de rentabilidad de una acción es igual al rendimiento real menos el rendimiento de un bono del Tesoro Utilizando datos mensuales desde septiembre de 2008 hasta agosto de 2013.), la siguiente imagen muestra los rendimientos superiores a la SP 500 en el eje horizontal, mientras que los rendimientos superiores a Coca-Cola están en el eje vertical.

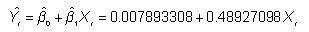
Se puede observar a partir de la gráfica de dispersión que esta relación es al menos aproximadamente lineal. Por lo tanto, la regresión lineal puede ser usada para estimar la relación entre estas dos variables.

Paso 3: Compruebe enfoques alternativos si las variables no son lineales

Si el dependiente especificada (Y) y las variables independientes (X) No tenemos una relación lineal entre ellas, puede ser posible transformar estas variables de manera que tienen una relación lineal. Por ejemplo, puede ser que la relación entre el logaritmo natural de Y y X es lineal. Otra posibilidad es que la relación entre el logaritmo natural de Y y el logaritmo natural de x es lineal. También es posible que la relación entre la raíz cuadrada de Y y X es lineal.

Si estas transformaciones no producen una relación lineal, las variables independientes alternativas que se pueden elegir mejor explicar el valor de la variable dependiente.

Paso 4: Estimar el modelo

El modelo de regresión lineal estándar se puede estimar con una técnica conocida como ordinaria como mínimo plazas. Esto se traduce en fórmulas para la pendiente y la intersección de la ecuación de regresión que "encajan" la relación entre la variable independiente (X) y la variable dependiente (Y) lo más cerca posible.

Por ejemplo, las siguientes tablas muestran los resultados de la estimación de un modelo de regresión para los rendimientos superiores a Coca-Cola de valores y el SP 500 en el período septiembre 2008 a agosto de 2013.

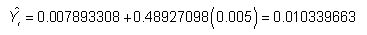
En este modelo, los rendimientos superiores a Coca-Cola de valores son la variable dependiente, mientras que los rendimientos superiores a la SP 500 son la variable independiente. En la columna de los coeficientes, se puede observar que el intercepto estimado de la ecuación de regresión es 0,007893308, y la pendiente estimada es de 0,48927098.

Pasos 5: Pruebe el ajuste del modelo utilizando el coeficiente de variación

El coeficiente de variación (también conocido como R²) Se utiliza para determinar cómo de cerca un modelo de regresión "encaja" o explica la relación entre la variable independiente (X) y la variable dependiente (Y). R² puede asumir un valor entre 0 y 1- cuanto más cerca R² es 1, mejor es el modelo de regresión explica los datos observados.

Como se muestra en las tablas de la Etapa 4, el coeficiente de variación se muestra como "R-Cuadrado" - esto es igual a 0,271795467. El ajuste no es particularmente fuerte. Lo más probable, el modelo es incompleto, como factores distintos de los rendimientos superiores a la SP 500 también determinar o explicar el exceso de rentabilidad a Coca-Cola de valores.

Para un modelo de regresión múltiple, el coeficiente de determinación ajustado se utiliza en lugar del coeficiente de determinación para probar el ajuste del modelo de regresión.

Paso 6: Realizar una prueba de hipótesis conjunta de los coeficientes

Una ecuación de regresión múltiple se utiliza para estimar la relación entre una variable dependiente (Y) y dos o más variables independientes (X). Cuando se implementa un modelo de regresión múltiple, la calidad global de los resultados puede comprobarse con una prueba de hipótesis. En este caso, la hipótesis nula es que todos los coeficientes cero pendiente de la igualdad de modelo, con la hipótesis alternativa de que al menos uno de los coeficientes de pendiente no es igual a cero.

Si esta hipótesis no puede ser rechazada, las variables independientes hacen no explicar el valor de la variable dependiente. Si la hipótesis es rechazada, al menos una de las variables independientes hace explicar el valor de la variable dependiente.

Paso 7: Realizar pruebas de hipótesis sobre los coeficientes de regresión individuales

Cada coeficiente estimado en una ecuación de regresión debe ser probado para determinar si es estadísticamente significativa. Si un coeficiente es estadísticamente significativa, la variable correspondiente ayuda a explicar el valor de la variable dependiente (Y). La hipótesis nula de que está siendo probado es que el coeficiente es igual a cero si esta hipótesis no puede ser rechazada, la variable correspondiente es no Estadísticamente significante.

Este tipo de prueba de hipótesis se puede realizar con un p-valor (también conocido como valor de probabilidad.) Las tablas de Paso 4 muestran que el p-valor asociado con el coeficiente de la pendiente es 1.94506 E-05. Esta expresión se escribe en términos de notación cientifica- también se puede escribir como 1,94506 X 10^-5 o 0,0000194506.

El p-valor se compara con el nivel de significación de la prueba de hipótesis. Si el valor p es menos que el nivel de significación, la hipótesis nula de que el coeficiente es igual a cero es rejected- la variable es, por lo tanto, estadísticamente significativa.

En este ejemplo, el nivel de significación 0,05 es. El valor de p de 0,0000194506 indica que la pendiente de esta ecuación es estadísticamente significativo- por ejemplo, el exceso regresa a la SP 500 explican los rendimientos superiores a Coca-Cola de valores.

Paso 8: Compruebe si hay violaciónes de los supuestos del análisis de regresión

El análisis de regresión se basa en varios supuestos clave. Violaciónes de estos supuestos puede dar lugar a resultados inexactos. Tres de las violaciónes más importantes que se pueden encontrar son conocidos como: autocorrelación, heterocedasticidad y multicolinealidad.

• Autocorrelación resulta cuando los residuos de un modelo de regresión no son independientes el uno del otro. (A residual es igual a la diferencia entre el valor de Y predicho por una ecuación de regresión y el valor real de Y.)

  Autocorrelación se puede detectar desde las gráficas de los residuales o utilizando medidas estadísticas más formales como el estadístico de Durbin-Watson. Autocorrelación se puede eliminar con transformaciones apropiadas de las variables de regresión.

• Heteroscedasticidad se refiere a una situación en la que las varianzas de los residuos de un modelo de regresión no son iguales. Este problema se puede identificar con una parcela de las transformaciones residuals- de los datos a veces se puede utilizar para superar este problema.

• Multicolinealidad es un problema que puede surgir solamente con el análisis de regresión múltiple. Se refiere a una situación en la que dos o más de las variables independientes están altamente correlacionados entre sí. Este problema se puede detectar con medidas estadísticas formales, tales como el factor de inflación de la varianza (VIF). Cuando multicolinealidad está presente, una de las variables altamente correlacionados deben ser removidos de la ecuación de regresión.

Paso 9: Interpretar los resultados

El intercepto estimado y el coeficiente de un modelo de regresión se pueden interpretar de la siguiente manera. La intersección muestra lo que el valor de Y sería si X fuera igual a cero. La pendiente muestra el impacto en Y de un cambio en X.

En base a las tablas en el paso 4, el intercepto estimado es de 0,007893308. Esto indica que el exceso de rentabilidad mensual para Coca-Cola Stock sería 0.007893308 o 0,7893308 por ciento, si el exceso de rentabilidad mensual al SP 500 eran del 0 por ciento.

Además, la pendiente estimada es de 0,48927098. Esto indica que un aumento del 1 por ciento en el exceso de rentabilidad mensual al SP 500 se traduciría en un aumento 0.48927098 por ciento en el exceso de rentabilidad mensual a Coca-Cola de valores. De manera equivalente, un 1 por ciento a disminuir el exceso de rentabilidad mensual al SP 500 se traduciría en una disminución 0.48927098 por ciento en el exceso de rentabilidad mensual a Coca-Cola de valores.

Paso 10: Pronóstico valores futuros

Un modelo de regresión estimado puede ser utilizado para producir previsiones del futuro valor de la variable dependiente. En este ejemplo, la ecuación estimada es:

Supongamos que un analista tiene razones para creer que el exceso de rentabilidad mensual al SP 500 en septiembre de 2013 será 0.005 o un 0,5 por ciento. La ecuación de regresión puede utilizarse para predecir el exceso de rentabilidad mensual a Coca-Cola de la manera siguiente:

El exceso de rentabilidad mensual pronosticado a Coca-Cola de valores es 0,010339663 o 1,0339663 por ciento.