Prueba de la ecuación de regresión estimada mediante el coeficiente de determinación, r2

Después de estimar la línea de regresión de la población, se puede comprobar si la ecuación de regresión tiene sentido utilizando el coeficiente de determinación, también conocido como R² (R al cuadrado). Esto se utiliza como una medida de lo bien que la ecuación de regresión en realidad describe la relación entre la variable dependiente (Y) Y la variable independiente (X).

Puede ser el caso de que no hay ninguna relación real entre la regresión simple variables- dependiente e independiente genera resultados incluso si este es el caso. Es, por lo tanto, es importante someter a los resultados de la regresión a algunas pruebas clave que le permiten determinar si los resultados son fiables.

El coeficiente de determinación, R², es una medida estadística que muestra la proporción de variación explicado por la recta de regresión estimada. Variación refiere a la suma de las diferencias al cuadrado entre los valores de Y y el valor medio de Y, expresado matemáticamente como

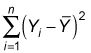
R² siempre toma un valor entre 0 y 1. Cuanto más cerca R² está a 1, mejor es la ecuación de regresión estimada se ajusta o explica la relación entre X y Y.

la expresión

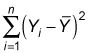
También se conoce como el suma total de cuadrados (TSS).

Esta suma se puede dividir en las dos siguientes categorías:

• Explicado suma de cuadrados (ESS): También conocido como el variación explicada, la ESS es la porción de la variación total que mide qué tan bien la ecuación de regresión explica la relación entre X y Y.

  Usted calcular la ESS con la fórmula

  

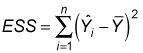
• Suma residual de cuadrados (RSS): Esta expresión es también conocida como variación no explicada y es la parte de la variación total que mide discrepancias (errores) entre los valores reales de Y y los estimados por la ecuación de regresión.

  Usted calcular el RSS con la fórmula

  

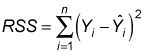
Cuanto menor sea el valor de RSS en relación con ESS, mejor es la línea de regresión se ajusta o explica la relación entre la variable dependiente e independiente.

• Suma total de cuadrados (TSS):

  La suma de RSS y ESS es igual a TSS.

  

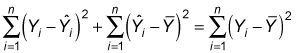
  R² es la relación entre la suma de los cuadrados explicada (ESS) a la suma total de cuadrados (SST):

  

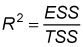
  También puede utilizar esta fórmula:

  

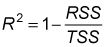
  Sobre la base de la definición de R², su valor no puede ser negativo. También, R² no puede ser mayor que 1, por lo

  

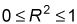
Con el análisis de regresión simple, R² es igual al cuadrado de la correlación entre X y Y.

El coeficiente de determinación se utiliza como una medida de lo bien que una línea de regresión explica la relación entre una variable dependiente (Y) Y una variable independiente (X). Cuanto más se acerca el coeficiente de determinación es 1, el la línea de regresión más estrechamente se ajusta a los datos de la muestra.

El coeficiente de determinación se calcula a partir de las sumas de cuadrados. Estos cálculos se resumen en la siguiente tabla.

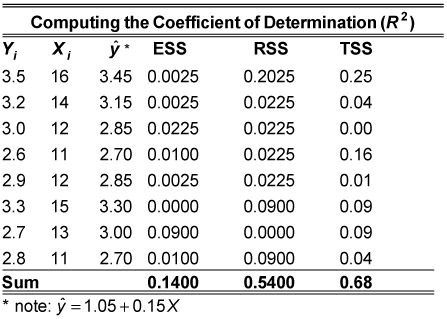
Para calcular ESS, se resta el valor medio de Y de cada uno de los valores estimados de Y- cada término se eleva al cuadrado y luego añadió juntos:

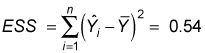
Para calcular RSS, se resta el valor estimado de Y de cada uno de los valores reales de Y- cada término se eleva al cuadrado y luego añadió juntos:

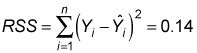
Para calcular TSS, se resta el valor medio de Y de cada uno de los valores reales de Y- cada término se eleva al cuadrado y luego añadió juntos:

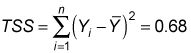
Alternativamente, usted puede agregar simplemente ESS y RSS para obtener TSS:

TSS = ESS + RSS = 0,54 + 0,14 = 0,68

El coeficiente de determinación (R²) Es la relación de ESS al TSS:

Esto demuestra que 79,41 por ciento de la variación en Y se explica por la variación en X. Debido a que el coeficiente de determinación no puede exceder de 100 por ciento, un valor de 79.41 indica que la línea de regresión coincide estrechamente los datos reales de la muestra.