Definir y justificar el principio de mínimos cuadrados
Cuando usted necesita para estimar una función de regresión muestra (SRF), el método econométrico más común es la técnica de mínimos cuadrados ordinarios (MCO), que utiliza los mínimos cuadrados principio para adaptarse a una función de regresión previamente especificado a través de los datos de la muestra.
los mínimos cuadrados prinprin- establece que la SRF debe ser construido (con los valores constantes y de pendiente) de manera que se minimiza la suma de la distancia al cuadrado entre los valores observados de la variable dependiente y los valores estimados de su SRF (el valor más pequeño posible).
Aunque los métodos a veces alternativas a OLS son necesarias, en la mayoría de situaciones, OLS sigue siendo la técnica más popular para la estimación de regresiones por las tres razones siguientes:
El uso de MCO es más fácil que las alternativas. Otras técnicas, incluyendo método generalizado de momentos (GMM) y máxima verosimilitud (ML) de estimación, se pueden utilizar para estimar funciones de regresión, pero requieren más sofisticación matemática y más potencia de cálculo. En estos días usted probablemente siempre tendrán todo el poder de computación que necesita, pero históricamente se limitaron la popularidad de otras técnicas en relación con la Operación.
OLS es sensato. Mediante el uso de residuos al cuadrado, puede evitar residuos positivos y negativos se anulen entre sí y encontrar una línea de regresión que es lo más cerca posible de los puntos de datos observados.
Resultados de MCO tienen características deseables. Un atributo deseable de cualquier estimador es para que sea un buen predictor. Cuando se utiliza OLS, las siguientes propiedades numéricas votos están asociados con los resultados:
La línea de regresión siempre pasa a través de medios de la muestra de Y y X o
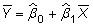
La media de la estimada (valor de referencia) Y valor es igual al valor medio de la actual Y o
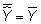
La media de los residuos es cero, o
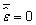
Los residuos no están correlacionados con el predicho Y, o
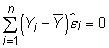
Los residuos no están correlacionados con los valores observados de la variable independiente, o
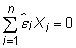
Las propiedades de MCO se utilizan para diversos pruebas en la econometría, pero también ilustran que sus predicciones serán perfectos, en promedio. Esta conclusión se desprende de la línea de regresión que pasa a través de las medias de la muestra, la media de sus predicciones igualando la media de los valores de los datos, y del hecho de que el promedio residual será cero.
Econometría: elección de la forma funcional de su modelo de regresión En la econometría, el procedimiento de estimación estándar para el modelo de regresión lineal clásica, mínimos cuadrados ordinarios (MCO), tiene capacidad para las relaciones complejas. Por lo tanto, usted tiene una cantidad considerable de…
Econometría para los maniquíes Técnicas econométricas se utilizan para estimar los modelos económicos, que en última instancia le permiten explicar cómo varios factores afectan a algunos resultados de interés o para pronosticar eventos futuros. La técnica de mínimos…
La estimación de la función de regresión y de los residuos La función de regresión se suele expresar matemáticamente en una de las siguientes maneras: notación básica, notación sumatoria o notación matricial. los Y variable representa el resultado que le interesa, llamada la variable dependiente, y…
Cómo comprobar si hay heteroscedasticidad mediante el examen de residuos graficadas En econometría, una manera informal de la comprobación de heteroscedasticidad es con un examen gráfica de los residuales. Si desea utilizar los gráficos para un examen de heterocedasticidad, primero elija una variable independiente que es…
Cómo desestacionalizar los datos de series de tiempo En muchos casos, los patrones estacionales se quitan de los datos de series de tiempo cuando están en libertad bajo las bases de datos públicas. Los datos que han sido despojados de sus patrones estacionales se conoce como seasonally ajustada o…
¿Cómo encontrar diferencias promedio utilizando una variable ficticia Usted debe recordar de su curso de estadística cómo llevar a cabo la t-prueba para examinar las diferencias de medias entre dos grupos. Pero lo que no saben es que se puede utilizar variables ficticias y análisis de regresión para obtener los…
Variables dependientes limitadas en la econometría Surgen variables dependientes limitadas cuando algún valor umbral mínimo debe alcanzar antes de que se observaron los valores de la variable dependiente y / o cuando algún valor umbral máximo restringe los valores observados de la variable…
Especificar el modelo de regresión de la econometría En la econometría, el modelo de regresión es un punto de partida común de un análisis. A medida que define el modelo de regresión, es necesario tener en cuenta varios elementos:La teoría económica, la intuición y el sentido común deben todo…
Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y la dirección de la relación entre dos o más variables. El…
¿Cómo las empresas utilizan las estadísticas de análisis de regresión El análisis de regresión es una herramienta estadística utilizada para la investigación de las relaciones entre las variables. Por lo general, el investigador desea saber el efecto causal de una variable sobre otra - el efecto de un aumento de…
Conocer las condiciones para la regresión Con la regresión lineal simple, usted busca un determinado tipo de relación entre dos variables cuantitativas (numéricas) (como GPA de escuela secundaria y la universidad GPA). Esta relación especial es un relación lineal - uno cuyos pares de…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…