Cómo estimar una tendencia en un modelo de regresión de series de tiempo

Para estimar un modelo de regresión de series de tiempo, una tendencia debe ser estimado. Se empieza por la creación de un gráfico de líneas de las series temporales. El gráfico de líneas muestra cómo una variable cambia con el tiempo- que puede ser utilizado para inspeccionar las características de los datos, en particular, para ver si existe una tendencia.

Por ejemplo, supongamos que usted es un administrador de cartera y tiene razones para creer una tendencia lineal se produce en una serie de tiempo de las declaraciones a las acciones de Microsoft. Trazar los precios mensuales desde agosto 2008 hasta julio 2013 en un gráfico como éste.

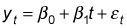
De acuerdo con esta figura, se produce ninguna tendencia en los datos. Los rendimientos suben y bajan sin un patrón particular.

Para probar formalmente si se produce una tendencia lineal, ejecutar una regresión de series de tiempo con una tendencia de tiempo como variable independiente, que se puede configurar de esta manera:

En este ejemplo, la variable dependiente es el precio de las acciones de Microsoft, y la variable independiente es el tiempo (en meses).

La siguiente figura muestra los resultados de este análisis de regresión.

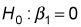
Para ejecutar esta regresión, la variable independiente (tiempo) se asigna valores numéricos de la siguiente manera. Asigne la primera fecha en la muestra un valor de 1, la segunda fecha de un valor de 2, y así sucesivamente. Así que para este ejemplo, asignar 08 2008 un valor de 1, septiembre de 2008 un valor de 2, y así sucesivamente de forma que la última observación en la muestra, julio de 2013, tiene un valor de 60.

Tenga en cuenta que en esta figura, el coeficiente de tiempo es no estadísticamente significativo- su valor p es de aproximadamente 0,6898. Para muchas pruebas de hipótesis, como regla general cualquier p-valor por encima de 0,05 indica que una variable no es estadísticamente significativa.

Más formalmente, la hipótesis nula

no puede ser rechazada al nivel del 5 por ciento de significancia. Esto significa que no hay pruebas suficientes para demostrar que hay una tendencia en los datos.

Cuando no hay tendencia, el valor de

Como otro ejemplo, suponga que en lugar de la estimación de una tendencia lineal de los rendimientos de las acciones de Microsoft, a estimar una tendencia lineal por el precio de las acciones de Microsoft. La siguiente figura muestra un gráfico de los precios mensuales de valores de Microsoft desde agosto 2008 a julio 2013.

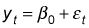
La siguiente figura muestra los resultados de ejecutar una regresión del precio de las acciones de Microsoft contra el tiempo con una tendencia lineal asumidos.

Los resultados muestran que la variable de tiempo es estadísticamente significativa al nivel del 5 por ciento (debido a que el valor de p para el tiempo es muy por debajo de 0,05). Sobre la base de los coeficientes en la figura, la ecuación de regresión estimada es

(Tenga en cuenta que los coeficientes se redondean en esta ecuación.) Esta ecuación muestra que durante el período de la muestra, el precio de las acciones de Microsoft creció en un promedio de $ 0,1975 por mes debido a 0,1975 es el coeficiente de t, y y se mide en dólares.

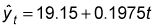
Supongamos que, en su papel como administrador de cartera desea determinar si una tendencia cuadrática ocurre en la serie histórica de precios de las acciones de Microsoft.

Si hay una tendencia cuadrática en una serie de tiempo, la ecuación de regresión es apropiada

Hay un nuevo término en esta ecuación:

Porque el tiempo se eleva al cuadrado aquí, este término capta la curvatura de la tendencia. Si este término es estadísticamente significativa, se dice que la tendencia asociada a esta serie de tiempo de tener un cuadrático tendencia.

La siguiente figura muestra los resultados de ejecutar esta regresión.

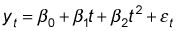
Esta figura muestra que el coeficiente de tiempo (t) Es estadísticamente significativo, mientras que el coeficiente de tiempo al cuadrado (t²) No lo es, lo que indica que hay no una tendencia cuadrática en los datos, pero hay una tendencia lineal. Por lo tanto, el precio de las acciones de Microsoft debería pronosticarse con el modelo de tendencia lineal: