¿Cómo clasificar las tendencias en un modelo de regresión de series de tiempo
Para estimar una serie de tiempo con el análisis de regresión, el primer paso es identificar el tipo de tendencia (si los hay) que está presente en los datos. El tipo de tendencia, tales como lineal o cuadrática, determina la ecuación exacta que se estima.
Sin tendencia
En el caso en el que una serie de tiempo no aumentar o disminuir con el tiempo, puede fluctuar en lugar al azar en torno a un valor constante. En este caso, la serie de tiempo tiene ninguna tendencia. La ecuación de tendencia se fija igual a una constante, que es la intersección de una ecuación de regresión:
La ecuación de regresión correspondiente es
Cuando se produce ninguna tendencia, los valores de la serie de tiempo pueden subir o bajar, pero en promedio tienden a volver al mismo nivel
Esta figura muestra una serie temporal sin tendencia.
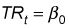
Observe que los valores de Y están aumentando de forma aleatoria y falling- no hay un patrón claro en los datos.
Tendencia lineal
Con una tendencia lineal, los valores de una serie de tiempo tienden a subir o bajar a una velocidad constante
La tendencia lineal se expresa como
La ecuación de regresión correspondiente es
La siguiente figura muestra una serie de tiempo con una tendencia lineal positiva. Con este tipo de tendencia, la variable independiente yt aumenta a una tasa constante en el tiempo. (Si una serie de tiempo tiene una tendencia lineal negativa, la variable independiente yt disminuye a una tasa constante en el tiempo).
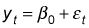
Tenga en cuenta que como t aumentos (tales como el tiempo transcurrido), Y tiende a aumentar en promedio. La línea de tendencia trazada a través de los valores de Y tiene una pendiente positiva, lo que indica que Y tiene una tendencia lineal positiva.
Tendencia cuadrática
Con una tendencia cuadrática, los valores de una serie de tiempo tienden a subir o bajar a una velocidad que no está Constant cambia con el tiempo. Como resultado, la tendencia no es una línea recta. La tendencia se expresa como
La ecuación de regresión correspondiente es
La siguiente figura muestra una serie de tiempo con una tendencia cuadrática. En este caso, el valor de yt aumenta a un ritmo creciente en el tiempo.
Tenga en cuenta que como t aumentos (tales como el tiempo transcurrido), Y tiende a aumentar a un ritmo creciente. La tendencia se curva upward- este tipo de curva indica que la Y tiene un positivo cuadrático tendencia.
Una ecuación cuadrática tiene al menos un cuadrado plazo. Por ejemplo, la siguiente es una ecuación de segundo grado:
Otras tendencias posibles
Es posible que la tendencia puede contener términos que se plantean a la tercera potencia, cuarto poder, o más alto. Este tipo de tendencia es muy poco frecuente en las aplicaciones de negocio. La mayoría de series de tiempo de los datos financieros tienen una tendencia lineal, una tendencia cuadrática, o ninguna tendencia en absoluto.
-
Pronosticar técnicas de análisis estadístico de datos grande -
Propiedades clave de una serie de tiempo en el análisis de datos -
Gráficos de dispersión: técnica gráfica de datos estadísticos -
Cómo tendencia de datos con un eje secundario en los informes de Excel -
Representar a las previsiones en sus componentes de tendencia en cuadros de mando de Excel -
Proyección de tendencias temporales con oles
Cómo estimar una tendencia en un modelo de regresión de series de tiempo Para estimar un modelo de regresión de series de tiempo, una tendencia debe ser estimado. Se empieza por la creación de un gráfico de líneas de las series temporales. El gráfico de líneas muestra cómo una variable cambia con el tiempo- que…
Cómo mostrar la relación entre dos variables utilizando un gráfico de dispersión LA gráfico de dispersión (también conocido como diagrama de dispersión) Muestra la relación entre dos variables cuantitativas) (numéricos. Estas variables pueden estar relacionadas positivamente, negativamente relacionada o no…
Cómo interpretar las líneas de tendencia, cuando el día de comercio Un analista técnico por lo general comienza por mirar un gráfico y dibujar líneas que muestran la dirección general de las barras de precios para el período en cuestión. En lugar de trazar la gráfica en papel o imprimir la pantalla,…
Cómo identificar las tendencias comerciales La identificación de una tendencia de comercio es relativamente sencillo. Instintivamente, lo sabrás cuando lo veas. Técnicas visuales e indicadores calculados ambos pueden ser utilizados para identificar señales de tendencias comerciales.Una…
Estrategia de inversión: tendencia seguidor o swing trader? Al analizar el mercado, usted puede elegir para ser una tendencia-seguidor o un columpio-comerciante. En el análisis técnico, la tendencia es siempre el foco. En un mundo perfecto, primero determinar si su seguridad está en tendencia o rango de…
¿Cómo saber cuándo la lectura barra de precios no funciona La lectura de los gráficos de barras no es siempre un proceso claro. En términos de barras, tendencia tiene dos identificadores - Una serie de máximos más altos (o bajos más bajos) y una serie de días (o día abajo). A veces, simplemente no…
Cómo utilizar una regresión lineal para identificar las tendencias del mercado En un gráfico de comercio, puede dibujar una línea (llamada línea de regresión lineal) Que pasa por el centro de la serie de precios, que se puede analizar para identificar las tendencias en el precio. Aunque no se puede técnicamente dibujar…
Cómo utilizar barras de precios para identificar una tendencia bajista En las finanzas, la observación central de análisis técnico es que la barra de precios encarna toda la dinámica de oferta y demanda del día y que una serie de barras en un gráfico muestra la evolución de la dinámica de oferta y demanda en el…
Determinar la fuerza de la tendencia cuando el comercio con la metodología de cinco de energía Después de determinar la dirección que desea para el comercio, a continuación, observa el indicador de momento para ver si el impulso (fuerza) está detrás de la tendencia. La tendencia, como lo demuestra el 50 SMA, le indica solamente la…
Averiguar cuál es la tendencia de comercio es El comercio de tendencia comienza con la determinación de la tendencia. los tendencia del mercado se define como la dirección a largo plazo del mercado. Pero, ¿cómo determinar lo que esa dirección es?Usted puede mirar en un gráfico y ver que…
Cómo utilizar varias escalas en el comercio Consultoría varios intervalos de tiempo del mismo mercado le ofrece una perspectiva diferente de una manera similar que se puede ver en un objeto con el ojo desnudo o con un microscopio. La ampliación se utiliza en el estudio de ese objeto le…
Identificar la tendencia cuando el comercio con la metodología de cinco de energía La primera decisión que tome con el método de cinco de energía es si vas a ir de largo, ir en corto, o mantenerse al margen. Tendencia simplemente se refiere a la dirección del mercado - arriba, abajo, o hacia los lados.Comercio en la dirección…