Proyección de tendencias temporales con oles

La mayoría de las series de tiempo económicas crecen con el tiempo, pero a veces las series temporales en realidad disminuyen con el tiempo. En cualquier caso, usted está buscando en una tendencia en el tiempo. Los modelos más comunes captura de tendencias en el tiempo son o bien lineal o exponencial.

Si la variable dependiente tiene un aumento relativamente constante en el tiempo, lo mejor es modelar la relación con una tendencia temporal lineal. Sin embargo, si el tasa de crecimiento es bastante constante (mientras que la velocidad a la que el valor de los cambios de variable dependiente no es constante), entonces usted necesita para modelar la relación con una tendencia en el tiempo exponencial.

• Una tendencia tiempo lineal tiene la forma

  

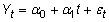
  dónde t es la variable de tendencia en el tiempo (normalmente una numeración secuencial de los períodos de tiempo que comienzan con un valor de 1) y

  

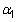
  es el coeficiente de tendencia en el tiempo y representa la velocidad a la que la valor de los cambios en la variable dependiente, en promedio, en cada periodo de tiempo posterior. Si el coeficiente de tendencia en el tiempo es, entonces los dependientes aumentos variables positivas a través del tiempo. Si el coeficiente de tendencia en el tiempo es negativo, entonces la variable dependiente disminuye con el tiempo.

• Puede expresar una tendencia temporal exponencial

  

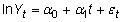
  dónde t es la variable de tendencia temporal y

  

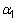
  es el coeficiente de tendencia en el tiempo y representa la velocidad a la que la crecimiento de los cambios en la variable dependiente, en promedio, en cada periodo de tiempo posterior. Si el coeficiente de tendencia en el tiempo es positivo, entonces la tasa de crecimiento de la variable dependiente es positivo en el tiempo. Si el coeficiente de tendencia en el tiempo es negativo, entonces la tasa de crecimiento de la variable dependiente es negativo en el tiempo.

La figura muestra un gráfico STATA de los inventarios anuales de 1950 a 1991 y un modelo de tendencia en el tiempo estimado. La mayoría de los conjuntos de datos no contienen una variable de tiempo, por lo que se pueden ordenar los datos utilizando la variable que captura la secuencia de las observaciones (años) y crear la variable tiempo.

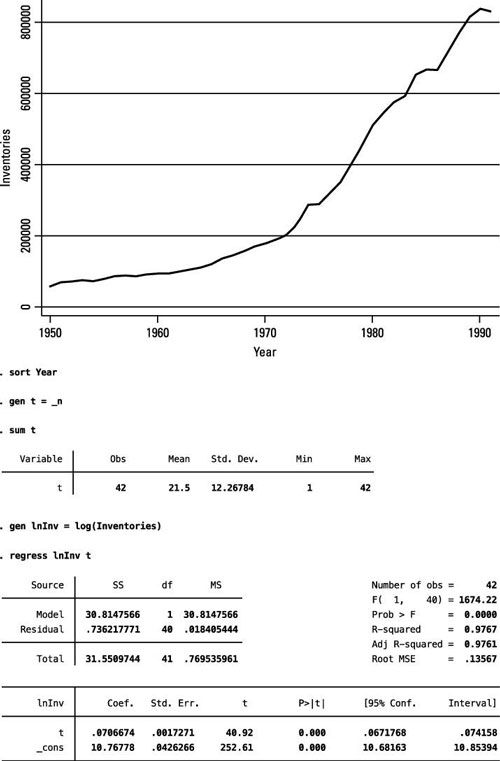
Dada la representación de las series de tiempo, aplicando el modelo de tendencia tiempo exponencial es más apropiado en este caso. El valor estimado de 0,07 para

implica que, en promedio, los inventarios han crecido a un ritmo de aproximadamente el 7 por ciento anual.

En el ejemplo, la creación de la variable de tendencia es un procedimiento sencillo, ya que sólo hay una variable de tiempo. Pero en algunos casos, existen múltiples variables de tiempo. Por ejemplo, con datos mensuales que se extiende por varios años, los datos es probable que contenga un curso y meses variable. En ese caso, usted desea ordenar tanto por años y meses antes de crear la variable de tendencia.

Cuando se trata de observaciones medidos durante varios períodos de tiempo, el valor de la variable de tendencia siempre debe representar el fin de la observación en una secuencia cronológica.

Si desea evitar el uso de una transformación registro de su variable dependiente (tal vez no parece apropiada con los otros factores que hemos incluido en el modelo como variables independientes), a continuación, una tendencia temporal cuadrática también puede funcionar bien en situaciones donde la tendencia en el tiempo no es lineal.

Aunque polinomios de orden superior se podrían utilizar para su tendencia en el tiempo, no son populares entre los econometristas aplicadas porque son difíciles de justificar teóricamente y por lo general consumen grados de libertad adicionales sin aumentar significativamente el poder explicativo.