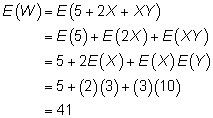Cómo hacer generalizaciones en la econometría con valor esperado o media
En la econometría, el valor esperado (o media) de una variable aleatoria proporciona una medida de tendencia central, lo que significa que proporciona una medición de donde los datos tiende a agruparse.
El valor esperado es el promedio de una variable aleatoria. Si usted tiene una variable aleatoria discreta, se puede calcular el valor esperado con la ecuación
dónde X representa los diferentes valores posibles para la variable aleatoria, y F(X) Es la probabilidad de que ocurra cada valor.
Si usted tiene una variable aleatoria continua, entonces calcular el valor esperado con esta ecuación:
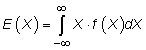
Aunque puede que tenga que reconocer la diferencia entre variables aleatorias discretas y continuas, probablemente no tendrá que realizar los cálculos manuales del valor esperado para las variables aleatorias continuas. Usted debe, sin embargo, saber cómo realizar cálculos manuales para una variable aleatoria discreta.
Supongamos que usted está examinando variable aleatoria X con la distribución de probabilidad se muestra en las dos primeras columnas de la tabla. Usted puede encontrar el valor esperado multiplicando cada valor posible para X por su probabilidad de ocurrencia y luego agregando esos valores. Usted muestra esta operación en la tercera columna, que le da E(X) = 1,5.
| X | Probabilidad (f (X)) | X * f (X) |
|---|---|---|
| 0 | 0,125 | 0 |
| 1 | 0,375 | 0,375 |
| 2 | 0,375 | 0,750 |
| 3 | 0,125 | 0,375 |
| Total: | 1 | 15 |
Si usted está manipular ecuaciones que contienen un operador valor esperado, encontrará los siguientes cinco propiedades útiles:
El valor esperado de una constante es la constante de sí mismo: E(la) = la
El valor esperado de dos variables aleatorias añadido juntos es igual a la suma de cada uno de sus valores esperados: E(X + Y) = E(X) + E(Y)
El valor esperado de una variable aleatoria multiplicado por una constante es igual a la constante multiplicada por el valor esperado de la variable aleatoria: E(aX) = aE(X)
Si X y Y son variables aleatorias independientes, entonces el valor esperado de su producto es igual al producto de sus valores esperados: E(XY) = E(X)E(Y)
Si X y Y son variables aleatorias independientes, entonces el valor esperado de su relación es igual a la relación de sus valores esperados:
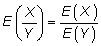
Supongamos que usted crea una variable aleatoria W definido por W = 5 + 2X + XY, donde la variable aleatoria X tiene un valor esperado igual a 3, la variable aleatoria Y tiene un valor esperado igual a 10, y son variables aleatorias independientes. Usando las propiedades de valor esperado, se calcula el valor esperado de W como
-
Bivariado o probabilidad conjunta densidad y la econometría -
Econometría y la función de densidad acumulativa (CDF) -
Econometría y la función de densidad de probabilidad (pdf) -
Cómo predecir el futuro con la densidad de probabilidad condicional -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal
Economía de la empresa: cómo crear el mejor del peor caso La teoría de la economía empresarial de criterios regret maxi-min y mini-max para las decisiones de negocio tiene que ver con la esperanza de lo mejor, pero esperando lo peor. Estos dos criterios de decisión se centran en el peor resultado…
La determinación de la media de una variable aleatoria discreta Cuando se trabaja con variables aleatorias, debe ser capaz de calcular e interpretar la media. Para estos problemas, y mucho X ser el número de clases tomadas por un estudiante universitario en un semestre. Utilice la fórmula para la media de una…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo definir una variable estadística aleatoria En estadística, un variable al azar es una característica, medida o recuento que cambia aleatoriamente de acuerdo con un determinado conjunto o patrón. Variables aleatorias son generalmente denotan con letras mayúsculas como X, Y, Z,…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
Cómo identificar una distribución muestral En estadística, una distribución de muestreo se basa en promedios de la muestra en lugar de los resultados individuales. Esto hace que sea diferente de una distribución. He aquí por qué: A variable al azar es una característica de interés que…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
Cómo indicar posibles resultados de una variable aleatoria discreta Una variable aleatoria discreta X puede tomar en un determinado conjunto de resultados posibles, y cada uno de esos resultados tiene una cierta probabilidad estadística de que se produzcan. La notación utilizada para cualquier resultado…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
Cómo utilizar el operador de suma para calcular el valor esperado Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…