Reconociendo las variables habituales: distribución normal
En econometría, una variable aleatoria con una distribución normal tiene una función de densidad de probabilidad de que es continsuperfluo, simétrico, y encampanado. Aunque muchas variables aleatorias pueden tener una distribución en forma de campana, la función de densidad de una distribución normal es precisamente
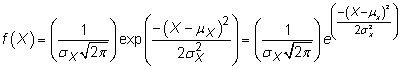
dónde
representa la media de la variable aleatoria distribuida normalmente X,
es la desviación estándar, y
representa la varianza de la variable aleatoria distribuida normalmente.
Una forma abreviada de lo que indica que una variable aleatoria, X, tiene una distribución normal es escribir
Una característica distintiva de una distribución normal es la probabilidad (o densidad) asociado con segmentos específicos de la distribución. La distribución normal en la figura está dividida en los intervalos más comunes (o segmentos): uno, dos, y tres desviaciones estándar de la media.
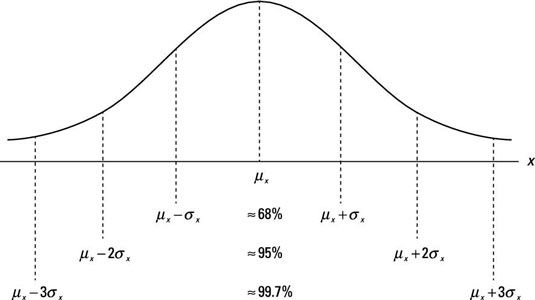
Con una variable aleatoria normalmente distribuida, aproximadamente el 68 por ciento de las mediciones están dentro de una desviación estándar de la media, el 95 por ciento son dentro de dos desviaciones estándar, y el 99,7 por ciento son dentro de tres desviaciones estándar.
Suponga que tiene los datos para toda la población de individuos que viven en residencias de ancianos. Descubres que la edad media de estas personas es de 70, la varianza es 9
y la distribución de su edad es normal. El uso de la taquigrafía, sólo podía escribir esta información
Si selecciona al azar a una persona de esta población, ¿cuáles son las posibilidades de que él o ella es más de 76 años de edad?
Utilizando la densidad de una distribución normal, usted sabe que aproximadamente el 95 por ciento de las mediciones tienen entre 64 y 76
(observe que 6 es igual a dos desviaciones estándar). El 5 por ciento restante son personas que tienen menos de 64 años de edad o más de 76. Debido a una distribución normal es simétrica, se puede concluir que usted tiene alrededor de un 2,5 por ciento (5% / 2 = 2,5%) la posibilidad de que se selecciona al azar alguien que es más de 76 años de edad.
Si una variable aleatoria es una combinación lineal de otra variable aleatoria distribuida normalmente (s), también tiene una distribución normal.
Suponga que tiene dos variables aleatorias descritas por estos términos:
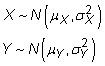
En otras palabras, variable aleatoria X tiene una distribución normal con una media de
y la varianza de
y variable aleatoria Y tiene una distribución normal con una media de
y una varianza de
Si crea una nueva variable aleatoria, W, como la siguiente combinación lineal de X y Y, W = aX + POr, después W También tiene una distribución normal. Además, el uso de valor y varianza propiedades esperadas, se puede describir la nueva variable aleatoria con esta notación abreviada:
-
Distribuciones de probabilidad en el análisis estadístico de datos grande -
Econometría y la función de densidad de probabilidad (pdf) -
Econometría y la distribución t -
Cómo hacer generalizaciones en la econometría con valor esperado o media -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
La distribución chi-cuadrado en la econometría
Estadísticas de las empresas: rendimientos de los activos de modelado con distribución normal Mparticipantes ercado - analistas de renta variable, los gestores de riesgos, los gestores de carteras, los comerciantes y los economistas - deben ser capaces de medir con precisión y modelar el riesgo y el rendimiento de los activos financieros.…
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
El empleo de la regla empírica en problemas estadísticos La regla empírica en las estadísticas establece que para una distribución normal, casi todos los datos caerán dentro de tres desviaciones estándar de la media. Use la regla empírica para resolver los siguientes problemas.Ejemplos de…
Cómo el número de grados de libertad afecta a la gráfica de una distribución t Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…
Cómo identificar una distribución muestral En estadística, una distribución de muestreo se basa en promedios de la muestra en lugar de los resultados individuales. Esto hace que sea diferente de una distribución. He aquí por qué: A variable al azar es una característica de interés que…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
Cómo indicar posibles resultados de una variable aleatoria discreta Una variable aleatoria discreta X puede tomar en un determinado conjunto de resultados posibles, y cada uno de esos resultados tiene una cierta probabilidad estadística de que se produzcan. La notación utilizada para cualquier resultado…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Haciendo cálculos cuando se conocen las desviaciones estándar poblacionales Cuando nos fijamos en la diferencia entre dos medias (o dos proporciones), realizar un seguimiento de lo que las poblaciones que está llamando Población 1 y Población 2. Restar dos números en el orden opuesto cambia el signo de los…