Cómo el número de grados de libertad afecta a la gráfica de una distribución t
Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las colas de la distribución t disminuye mientras que el área cerca del centro aumenta. (Las colas consisten en los valores extremos de la distribución, tanto negativos como positivos.) Finalmente, cuando los grados de libertad alcanza 30 o más, el t-distribución y la distribución normal estándar son extremadamente similares.
Las siguientes figuras ilustran la relación entre la distribución t con diferentes grados de libertad y la distribución normal estándar. La primera figura muestra el nivel normal y la distribución t con dos grados de libertad (df). Observe cómo la distribución t es significativamente más hacia fuera que la distribución normal estándar.
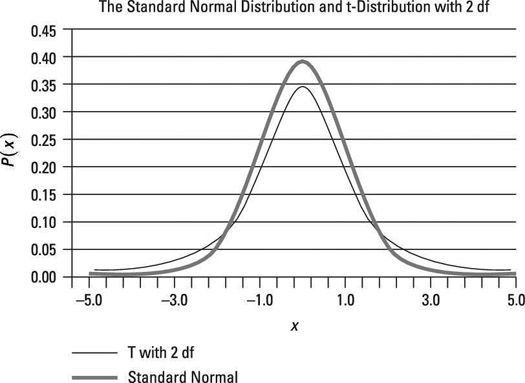
El gráfico de la primera figura muestra que la distribución t tiene más superficie en las colas y menos área alrededor de la media de la distribución normal estándar. (La curva de distribución normal estándar se muestra con marcadores cuadrados.) Como resultado, las observaciones más extremas (positivos y negativos) es probable que se produzca en la distribución t que bajo la distribución normal estándar.
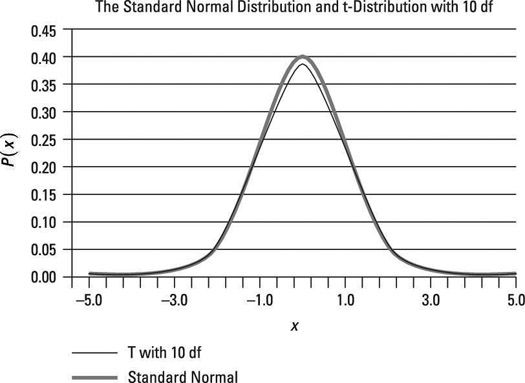
La segunda cifra se compara la distribución normal estándar con la distribución t con diez grados de libertad. Los dos son mucho más cerca uno del otro aquí que en la primera figura.
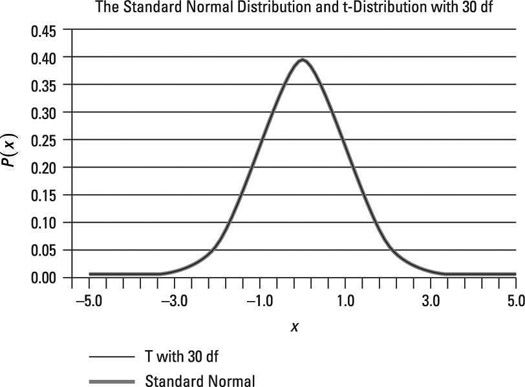
Como se puede ver en la tercera figura, con 30 grados de libertad, la distribución t y la distribución normal estándar son casi indistinguibles.
-
Econometría y la distribución t -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal -
La distribución chi-cuadrado en la econometría -
La distribución f en la econometría -
Estadísticas de las empresas: rendimientos de los activos de modelado con distribución normal
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una pequeña muestra Cuando se utiliza una pequeña muestra para probar una hipótesis acerca de una media poblacional, se toma el valor crítico resultante o los valores de la distribución t de Student. Para una prueba de dos colas, el valor crítico esy n representa…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande En estadística, una amplia muestra tiene un tamaño mayor o igual a 30. Cuando se utiliza una gran muestra para probar una hipótesis acerca de una media poblacional, el valor o valores críticos resultante de dos colas de la distribución normal…
Cómo una distribución normal afecta a la forma de una distribución de muestreo En las estadísticas, cuando la distribución original para una población X es normal, entonces usted también puede asumir que la forma de la distribución de muestreo, oTambién será normal, independientemente del tamaño de muestra n.Por…
¿Cómo se ve afectada una distribución de muestreo cuando la distribución no es normal En estadística, si una población X tiene cualquier distribución que es no lo normal, o si su distribución es desconocida, no se puede decir de forma automática la distribución de las medias de la muestratiene una distribución normal. Pero…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar los valores críticos para una hipótesis de ANOVA utilizando el f-mesa Usted puede encontrar los valores críticos para una hipótesis de ANOVA utilizando la mesa F. Debido a que la distribución F se basa en dos tipos de grados de libertad, hay una tabla para cada posible valor de alfa (el nivel de significación).La…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Distribuciones estadísticas: binomial, y t-distribución normal Una distribución estadística es una lista de los posibles valores de una variable (o intervalos de valores) y la frecuencia (o en qué densidad) que se produzcan. Se puede tomar varias formas, incluyendo binomial, normal, y t-distribución.LA…