Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t
Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):
El primer momento de una distribución es el valor esperado, E(X), Que representa el valor medio o promedio de la distribución.
Para la distribución t con
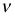
grados de libertad, la media (o valor esperado) es igual
o una distribución de probabilidad, y
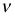
comúnmente designa el número de grados de libertad de una distribución.
El segundo momento central es la varianza
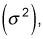
y que mide la dispersión de la distribución sobre el valor esperado. El más extendido una distribución, más "estirado" es la gráfica de la distribución. En otras palabras, las colas estarán más lejos de la media, y la zona cerca de la media serán más pequeños. Por ejemplo, en base a las siguientes figuras, se puede observar que la distribución t con 2 grados de libertad es mucho más hacia fuera que la distribución t con 30 grados de libertad.
Se utiliza la fórmula
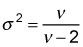
para calcular la varianza de la distribución t.
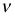La distribución t normal y estándar con dos grados de libertad.La distribución-t normal y estándar con 30 grados de libertad.
A modo de ejemplo, con 10 grados de libertad, la varianza de la distribución t se calcula mediante la sustitución de 10 por
en la fórmula de la varianza:
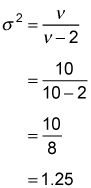
Con 30 grados de libertad, la varianza de la distribución t es igual
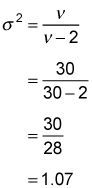
Estos cálculos muestran que a medida que los grados de libertad, se incrementa la varianza de los descensos t-distribución, consiguiendo progresivamente más cerca de 1.
La desviación estándar es la raíz cuadrada de la varianza
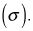
(No es un momento separado.)
Para la distribución t, se encuentra la desviación estándar con esta fórmula:
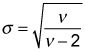
Para la mayoría de aplicaciones, la desviación estándar es una medida más útil que la varianza porque la desviación estándar y el valor esperado se miden en las mismas unidades, mientras que la varianza se mide en cuadrado unidades. Por ejemplo, supongamos que usted asume que la rentabilidad de una cartera siguen la distribución t. Usted mide tanto el valor esperado de las devoluciones y la desviación estándar como porcentaje- se mide la varianza como cuadrado porcentaje, que es un concepto difícil de interpretar.
-
Econometría y la distribución t -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal -
La distribución chi-cuadrado en la econometría -
La distribución f en la econometría -
Encuentra las pruebas estadísticas apropiadas para dos poblaciones independientes de igual tamaño y varianza
Cómo el número de grados de libertad afecta a la gráfica de una distribución t Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…
Cómo calcular la varianza y la desviación estándar en la distribución uniforme los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el…
Cómo cambiar un valor de x para un valor z Si usted tiene una muestra estadística con una distribución normal, se puede conectar un X-valor para esta distribución en una ecuación especial para encontrar su z-valor. los z-valor, entonces puede ayudar a interpretar los valores…
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…