¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial
Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes resultados son lo que salió de ella.
Si X tiene una distribución binomial con n ensayos y probabilidad de éxito p en cada ensayo, entonces:
La media de X es
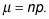
La varianza de X es
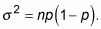
La desviación estándar de X es
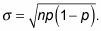
Por ejemplo, supongamos que usted lanza una moneda al aire 100 veces y dejar X ser el número de cabezas- entonces X tiene una distribución binomial con n = 100 y p = 0.50. Su media es
cabezas (que tiene sentido, porque si usted lanza una moneda 100 veces, que se puede esperar para obtener 50 cabezas). La varianza de X es
que está en unidades cuadradas (lo que no puede interpretarlo) - y la desviación estándar es la raíz cuadrada de la varianza, que es 5. Eso significa que cuando se tira una moneda 100 veces, y hacer eso una y otra vez, el promedio número de cabezas que obtendrá es de 50, y se puede esperar que para variar por cerca de 5 cabezas en promedio.
La fórmula para la media de una distribución binomial tiene significado intuitivo. los p en la fórmula representa la probabilidad de un éxito, sí, pero también representa la proporción de los éxitos que puede esperar en n ensayos. Por lo tanto, el total número de los éxitos que puede esperar - es decir, la media de X - es
La fórmula para la varianza tiene algo de un significado intuitivo también. La única variación en los resultados de cada ensayo es entre el éxito (con probabilidad p) Y la insuficiencia (con probabilidad 1 - p). Encima n ensayos, se mide la variación del número de éxitos / fracasos por
La desviación estándar es la raíz cuadrada.
-
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Encontrar probabilidades binomiales con una fórmula -
Cómo calcular las probabilidades geométricas -
Cómo calcular la desviación estándar de un conjunto de datos estadísticos -
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t -
Cómo calcular la varianza y la desviación estándar en la distribución uniforme
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…
Cómo identificar una variable aleatoria binomial La variable aleatoria discreta más conocido y amado en las estadísticas es el binomio. Binomial medio dos nombres y se asocia con situaciones que participen dos resultados- por ejemplo, sí / no, o el éxito / fracaso (golpear una luz roja o no,…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
Cómo saber cuando una variable aleatoria no tiene una distribución binomial Con el fin de saber cuándo una variable aleatoria de una muestra estadística no tiene una distribución binomial, primero tiene que saber lo que hace que sea binomial. Puede identificar una variable aleatoria binomial como si se cumplen las cuatro…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
Distribuciones estadísticas: binomial, y t-distribución normal Una distribución estadística es una lista de los posibles valores de una variable (o intervalos de valores) y la frecuencia (o en qué densidad) que se produzcan. Se puede tomar varias formas, incluyendo binomial, normal, y t-distribución.LA…