¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística
Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas estadísticas establecidas para encontrar probabilidades binomiales, utilizando los valores de n y p única para cada problema.
Las probabilidades para una variable aleatoria binomial X se puede encontrar con la siguiente fórmula para p(X):
dónde
n es el número fijo de ensayos.
X es el número especificado de éxitos.
n - X es el número de fallos.
p es la probabilidad de éxito en cualquier ensayo dado.
1 - p es la probabilidad de fallo en cualquier ensayo dado. (Nota: Algunos libros de texto utilizan la letra q para denotar la probabilidad de fallo en lugar de 1 - p.)
Estas probabilidades son válidas para cualquier valor de X entre 0 (menor número de posibles éxitos en n ensayos) y n (número más alto de posibles éxitos).
El número de maneras de reorganizar X éxitos entre n ensayos se llama "n escoger X,"Y la notación es
Es importante señalar que esta expresión matemática no es un fraccionamiento que es la abreviatura de matemáticas para representar el número de maneras de hacer este tipo de reordenamientos.
En general, para calcular "n escoger X,"Se utiliza la siguiente fórmula:
La notación n! representa -n factorial, el número de formas para reorganizar n artículos. Calcular n!, multiplicas n(n - 1) (n - 2). . . (2) (1). Por ejemplo, 5! es 5 (4) (3) (2) (1) = 120- 2! es 2 (1) = 2 y 1! es 1. Por convención, 0! es igual a 1.
Suponga que tiene que cruzar tres semáforos en su camino al trabajo. Dejar X ser el número de luces rojas alcanze de los tres. ¿De cuántas maneras se puede golpear dos luces rojas en su camino al trabajo? (Para este ejemplo, se puede asumir que una luz amarilla equivale a un semáforo en rojo.) Bueno, usted podría golpear una verde primero, luego los otros dos rojos o usted podría golpear el verde en el centro y tienen los rojos para el primer y tercer luces, o usted podría golpear rojo primero, luego otro rojo, luego verde. Dejar G = verde y R = rojo, puede escribir estas tres posibilidades como: GRR, RGR, RRG. Así que usted puede golpear dos luces rojas en su manera de trabajar de tres maneras, ¿no?
Compruebe la matemáticas. En este ejemplo, un "juicio" es una iluminación de tráfico y un "éxito" es una luz roja. (Sí, eso parece raro, pero un éxito es lo que usted está interesado en contar, bueno o malo.) Así que tienes n = 3 luces de tráfico total, y usted está interesado en la situación en la que se obtiene X = 2 los rojos. Utilizando la notación de lujo,
significa "3 eligen 2" y representa el número de maneras de reorganizar 2 éxitos en 3 ensayos.
Para calcular "3 elegir 2," hace lo siguiente:
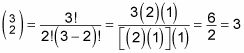
Esto confirma las tres posibilidades que figuran para conseguir dos luces rojas.
Ahora supongamos que las luces de funcionar de forma independiente el uno del otro y cada uno tiene una probabilidad del 30% de ser de color rojo. Supongamos que desea encontrar la distribución de probabilidad para X. (Es decir, una lista de todos los valores posibles de X - 0,1,2,3 - y sus probabilidades).
Antes de sumergirse en los cálculos, primero comprueba para ver si usted tiene una situación binomial aquí. Tienes n = 3 ensayos (semáforos) - comprobar. Cada prueba es el éxito (luz roja) o el fracaso (iluminación de color amarillo o verde, en otras palabras, la luz "no rojo") - comprobar. Las luces de funcionar de manera independiente, por lo que tiene las pruebas independientes atendidos, y porque cada luz es de color rojo 30% de las veces, usted sabe p = 0,30 para cada luz. Así X = Número de semáforos en rojo tiene una distribución binomial. Para rellenar los gritties nitty para las fórmulas, 1 - p = Probabilidad de que una luz no roja = 1-0,30 = 0.70- y el número de luces rojas no es 3 - X.
Usando la fórmula para p(X), A obtener las probabilidades de X = 0, 1, 2 y 3 luces rojas:
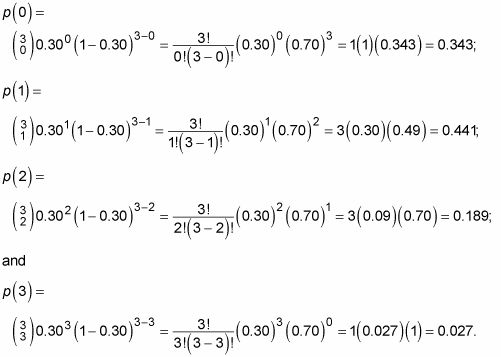
La distribución de probabilidad final para X se muestra en la siguiente tabla. Observe estas probabilidades toda suma de 1, porque cada valor posible de X aparece y representó.
Distribución de probabilidad para X = Número de Rojas Semáforos (n = 3, p = 0,30):
| X | p (x) |
|---|---|
| 0 | 0,343 |
| 1 | 0,441 |
| 2 | 0,189 |
| 3 | 0,027 |






