Calcular probabilidades binomiales utilizando la tabla binomial
Para los ejemplos de preguntas aquí, X es una variable aleatoria con una distribución binomial con n = 11 y p = 0,4. Utilice la tabla binomial para responder a los siguientes problemas.
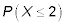
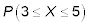
Ejemplos de preguntas
Que es P(X = 5)?
Responder: 0,221
La tabla binomial tiene una serie de mini-mesas dentro de él, uno para cada valor seleccionado de n. Encontrar P(X = 5), donde n = 11 y p = 0.4, busque el mini-mesa para n = 11, encuentre la fila para X = 5, y seguir hacia donde se cruza con la columna p = 0,4. Este valor es 0.221.
Que es P(X > 0)?
Responder: 0,996
Para encontrar la probabilidad de que X es mayor que 0, encuentre la probabilidad de que X es igual a 0, y luego restar esa probabilidad de 1. Esto hace que los cálculos mucho más fácil.
La tabla binomial tiene una serie de mini-mesas dentro de él, uno para cada valor seleccionado de n. Encontrar P(X = 0), donde n = 11 y p = 0.4, busque el mini-mesa para n = 11, encuentre la fila para X = 0, y seguir hacia donde se cruza con la columna p = 0,4. Este valor es 0.004. Ahora resta que a partir de 1:
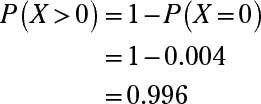
Que es
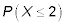
Responder: 0,120
Para encontrar la probabilidad de que X es menor o igual a 2, primero tiene que encontrar la probabilidad de cada posible valor de X inferior a 2. En otras palabras, a encontrar los valores para P(X = 0), P(X = 1), y P(X = 2).
Para encontrar cada una de estas probabilidades, utilice la tabla binomial, que tiene una serie de mini-mesas dentro de él, uno para cada valor seleccionado de n. Encontrar P(X = 0), donde n = 11 y p = 0.4, busque el mini-mesa para n = 11, encuentre la fila para X = 0, y seguir hacia donde se cruza con la columna p = 0,4. Este valor es 0.004.
Ahora haga lo mismo para las otras probabilidades: P(X = 1) = 0,027 y P(X = 2) = 0,089. Por último, añadir estas probabilidades juntos:
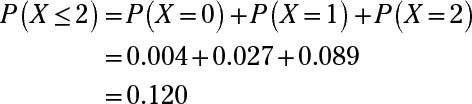
Que es P(X > 9)?
Responder: 0,001
Para encontrar la probabilidad de que X es mayor que 9, en primer lugar encontrar la probabilidad de que X es igual a 10 o 11 (en este caso, 11 es el mayor valor posible de X porque sólo hay 11 pruebas en total).
Para encontrar cada una de estas probabilidades, utilice la tabla binomial, que tiene una serie de mini-mesas dentro de él, uno para cada valor seleccionado de n. Encontrar P(X = 10), donde n = 11 y p = 0.4, busque el mini-mesa para n = 11, encuentre la fila para X = 10, y seguir hacia donde se cruza con la columna p = 0,4. Este valor es 0.001.
Ahora haga lo mismo para P(X = 11), que le da 0.000. (Nota: P (X = 11) no es exactamente 0.000 aquí- es sólo una probabilidad menor que se puede expresar en las cuatro posiciones decimales utilizadas en esta tabla) Por último, añadir las dos probabilidades juntos.:
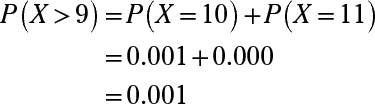
Que es
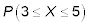
Responder: 0,634
Aquí, usted quiere encontrar la probabilidad igual a 3 y 5, y todo lo demás. En otras palabras, usted quiere las probabilidades de X = 3, X = 4, y X = 5. Usted sabe que n = 11 y p = 0,4, que es la probabilidad de éxito en cada intento.
Para encontrar cada una de estas probabilidades, utilice la tabla binomial, que tiene una serie de mini-mesas dentro de él, uno para cada valor seleccionado de n. Encontrar P(X = 3), donde n = 11 y p = 0.4, busque el mini-mesa para n = 11, encuentre la fila para X = 3, y seguir hacia donde se cruza con la columna p = 0,4. Este valor es 0.177.
Ahora haga lo mismo para las otras probabilidades: P(X = 4) = 0,236 y P(X = 5) = 0,221. Por último, añadir estas probabilidades juntos:
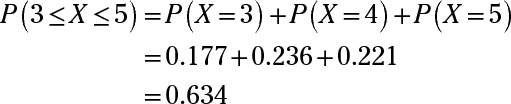
Si necesita más práctica sobre este y otros temas de su curso de estadística, visite 1.001 Estadísticas Entrenamiento Problemas para Dummies comprar acceso en línea a 1.001 problemas de práctica estadísticas! Podemos ayudarle a rastrear su rendimiento, ver dónde se necesita para estudiar y crear un problema personalizado establece para dominar sus habilidades de Estadísticas.
-
Bivariado o probabilidad conjunta densidad y la econometría -
Econometría y la función de densidad acumulativa (CDF) -
Cómo predecir el futuro con la densidad de probabilidad condicional -
Cómo leer y trabajar con tablas de probabilidad -
La determinación de la media de una variable aleatoria discreta -
Diferenciar entre distribuciones de probabilidad discretas y continuas
Encontrar probabilidades binomiales con una fórmula Aquí, se llega a practicar la búsqueda de probabilidades binomiales usando una fórmula. Los siguientes problemas tienen una variable aleatoria binomial con p = 0.55. Utilice las siguientes fórmulas para la distribución binomial para los…
Cómo calcular las probabilidades geométricas La distribución geométrica se basa en el proceso binomial (una serie de ensayos independientes con dos resultados posibles). Se utiliza la distribución geométrica para determinar la probabilidad de que un determinado número de pruebas se…
Cómo calcular las probabilidades de Poisson los Distribución de Poisson es útil para medir cómo pueden ocurrir muchos eventos durante un horizonte de tiempo dado, tal como el número de clientes que entran en una tienda durante la siguiente hora, el número de accesos a una página web…
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar probabilidades para z con la mesa de z Puede utilizar el Z-mesa para encontrar un conjunto completo de "-menos que" las probabilidades para una amplia gama de z-los valores. Para utilizar el Z-tabla para encontrar las probabilidades de una muestra estadística con una normal estándar…
¿Cómo encontrar probabilidades estadísticas en una distribución normal Si su muestra estadística tiene una distribución normal (X), Entonces usted puede utilizar el Z-mesa para encontrar la probabilidad de que algo va a ocurrir dentro de un conjunto definido de parámetros. Por ejemplo, usted podría mirar a la…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…
¿Cómo encontrar incondicionales, o marginales, probabilidades Un incondicional, o marginal, la probabilidad es uno donde los eventos (posibles resultados) son independientes entre sí. Cuando se crea un tabla de probabilidad conjunta, la probabilidad incondicional de un evento aparece como un total de fila o…
¿Cómo encontrar t *-valores para los intervalos de confianza Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…