Econometría y la función de densidad acumulativa (CDF)
los función de densidad acumulativa
(CDF) de una variable aleatoria X es el suma o devengo de probabilidades hasta cierto valor. Se muestra cómo la suma de las probabilidades se aproxima a 1, que a veces se produce a una velocidad constante y, a veces se produce a una velocidad cambiante.La CDF para variables aleatorias discretas
Para una variable aleatoria discreta, la CDF es equivalente a
dónde F(X) Es la función de densidad de probabilidad.
Si usted está observando una variable aleatoria discreta, la CDF puede describirse en una tabla o gráfico. Para construir una mesa, poner los valores posibles de la variable aleatoria en una columna, la probabilidad de que ocurran en otra columna, y las sumas de las probabilidades a cualquier valor dado en la tercera columna.
En una representación gráfica de la CDF, se colocan los posibles valores de la variable aleatoria en el eje horizontal, y la altura de una línea horizontal en cada valor muestra la probabilidad de que el valor sumado con las probabilidades de todos los valores más pequeños.
Supongamos que realiza un experimento que consiste en lanzar dos monedas al mismo tiempo. Usted está interesado en el número de veces que la moneda cae Heads Up, así que usted designa el número de caras observadas como mi variable aleatoria X. La tabla muestra los posibles resultados de este experimento y los valores para X generado a partir del proceso.
| Resultado | Primera Moneda | Segundo Coin | Número de Jefes, X |
|---|---|---|---|
| 1 | T | T | 0 |
| 2 | T | H | 1 |
| 3 | H | T | 1 |
| 4 | H | H | 2 |
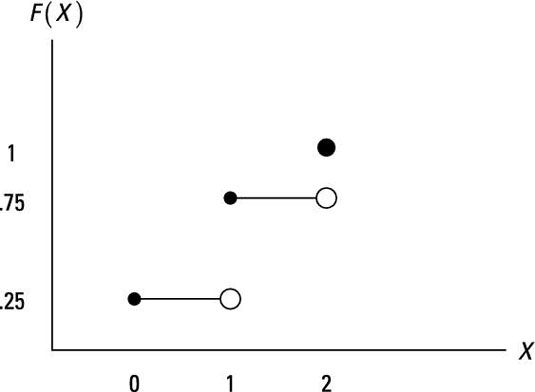
Puede resumir la información con una tabla o un gráfico de la CDF para X. La siguiente tabla muestra una forma de tabla de la CDF. Recordemos que el PDF, F(X), Representa la probabilidad de un evento aleatorio dado, y el CDF, F(X), Es la suma de las probabilidades a cualquier valor aleatorio.
Por ejemplo, F(X = 1) = 2/4 = 0,50 y F(X = 1) = 1/4 + 1/2 = 3 cuartos = 0,75.
| X | f (X) | F (X) |
|---|---|---|
| 0 | 0.25 | 0.25 |
| 1 | 0.50 | 0.75 |
| 2 | 0.25 | 1 |
La CDF para variables aleatorias continuas
¡Prepárate para el cálculo! El CDF es una suma de probabilidades, y para una función continua, la búsqueda de una suma significa integración. Integración es un procedimiento de cálculo que le permite encontrar densidades menores de funciones no lineales. Para una variable aleatoria continua, la CDF es
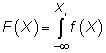
dónde F(X) Es la función de densidad de probabilidad.
Si usted está observando una variable aleatoria continua, la CDF se puede describir en una función o un gráfico. La función muestra cómo se comporta la variable aleatoria a través de cualquier rango posible de valores.
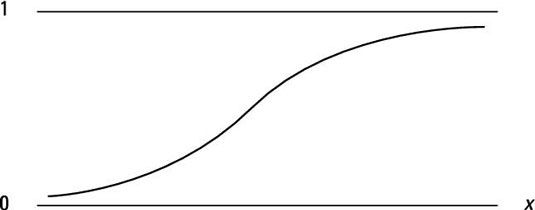
La forma precisa de la FCD depende de la media y la varianza (el cuadrado de la desviación estándar) de la variable aleatoria. Un medio menor desplaza la curva hacia la izquierda, y una media más grande desplaza la curva hacia la derecha. Una variación más pequeña hace que la curva más pronunciada, mientras que una variación más grande hace más plana curva.
-
Bivariado o probabilidad conjunta densidad y la econometría -
Econometría y la función de densidad de probabilidad (pdf) -
Cómo hacer generalizaciones en la econometría con valor esperado o media -
Cómo predecir el futuro con la densidad de probabilidad condicional -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal
Especificación de funciones no lineales apropiadas: los modelos probit y logit Si el resultado de interés es cualitativa, se utiliza una variable dependiente maniquí y estimar la probabilidad de que el resultado (Y = 1) se produce utilizando el modelo econométrico. Aunque OLS se pueden utilizar para estimar un modelo con…
La determinación de la media de una variable aleatoria discreta Cuando se trabaja con variables aleatorias, debe ser capaz de calcular e interpretar la media. Para estos problemas, y mucho X ser el número de clases tomadas por un estudiante universitario en un semestre. Utilice la fórmula para la media de una…
Diferenciar entre distribuciones de probabilidad discretas y continuas LA Distribución de probabilidad es una fórmula o una tabla utilizada para asignar probabilidades a cada posible valor de una variable aleatoria X. Una distribución de probabilidad puede ser o bien discreto o continua. Una distribución discreta…
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
¿Cómo definir una variable estadística aleatoria En estadística, un variable al azar es una característica, medida o recuento que cambia aleatoriamente de acuerdo con un determinado conjunto o patrón. Variables aleatorias son generalmente denotan con letras mayúsculas como X, Y, Z,…
¿Cómo encontrar probabilidades para z con la mesa de z Puede utilizar el Z-mesa para encontrar un conjunto completo de "-menos que" las probabilidades para una amplia gama de z-los valores. Para utilizar el Z-tabla para encontrar las probabilidades de una muestra estadística con una normal estándar…
Cómo identificar una variable aleatoria binomial La variable aleatoria discreta más conocido y amado en las estadísticas es el binomio. Binomial medio dos nombres y se asocia con situaciones que participen dos resultados- por ejemplo, sí / no, o el éxito / fracaso (golpear una luz roja o no,…
Cómo identificar una distribución muestral En estadística, una distribución de muestreo se basa en promedios de la muestra en lugar de los resultados individuales. Esto hace que sea diferente de una distribución. He aquí por qué: A variable al azar es una característica de interés que…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
Cómo indicar posibles resultados de una variable aleatoria discreta Una variable aleatoria discreta X puede tomar en un determinado conjunto de resultados posibles, y cada uno de esos resultados tiene una cierta probabilidad estadística de que se produzcan. La notación utilizada para cualquier resultado…
Cómo utilizar el operador de suma para calcular el valor esperado Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…