Econometría y la función de densidad de probabilidad (pdf)
LA la función de densidad de probabilidad
(PDF) muestra las probabilidades de una variable aleatoria para todos sus valores posibles. Las probabilidades asociadas con los valores específicos (o eventos) de una variable aleatoria deben adherirse a las propiedades
dónde Xj representa los valores posibles (resultados) de variable aleatoria X. En otras palabras, las posibilidades de cualquier evento aleatorio que ocurre deben estar en cualquier lugar de ser imposible (probabilidad de 0) para cierta (probabilidad de 1), y la suma de las probabilidades de todos los eventos debe ser 1 (o 100 por ciento).
El PDF para variables aleatorias discretas
Si usted está observando una variable aleatoria discreta, el PDF se puede describir en una tabla o gráfico. Para construir una tabla, se configura una columna con los valores posibles de la variable aleatoria y una columna con la probabilidad de que van a ocurrir.
En una representación gráfica del PDF (un gráfico de barras), que le coloca los posibles valores de la variable aleatoria en el eje horizontal, y la altura de las barras verticales en cada valor muestra la probabilidad de que se produzcan.
Supongamos que realiza un experimento que consiste en lanzar tres monedas al mismo tiempo. Usted está interesado en el número de veces que la tierra las cabezas para arriba, así que llame al número de cabezas observó variable aleatoria X. La tabla muestra los posibles resultados de este experimento y los valores para X generado a partir del proceso.
| Resultado | Primera Moneda | Segundo Coin | Tercer Coin | Número de Jefes, X |
|---|---|---|---|---|
| 1 | T | T | T | 0 |
| 2 | T | T | H | 1 |
| 3 | T | H | T | 1 |
| 4 | H | T | T | 1 |
| 5 | T | H | H | 2 |
| 6 | H | H | T | 2 |
| 7 | H | T | H | 2 |
| 8 | H | H | H | 3 |
Fuera de ocho resultados posibles, se obtiene 0 cabezas en un resultado, 1 cabeza con tres resultados, 2 cabezas en tres resultados, y 3 cabezas en un solo resultado. Puede resumir la información con una representación tabular o gráfica del PDF para X.
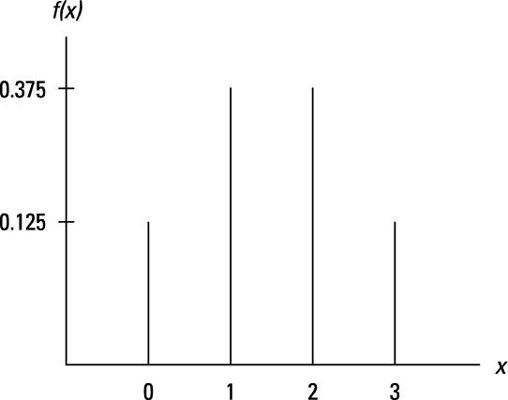
Ves 8 resultados totales y cuatro valores posibles para X: 0, 1, 2 y 3. Esta información le permite calcular la probabilidad asociada a cada X valor. Por ejemplo, X = 0 se produce sólo una vez, por lo que F(X = 0) = 1/8 = 0.125. La siguiente tabla muestra las probabilidades para el otro X valores y una forma de tabla del PDF.
| X | f (X) |
|---|---|
| 0 | 1/8 = 0.125 |
| 1 | 8.3 = 0.375 |
| 2 | 8.3 = 0.375 |
| 3 | 1/8 = 0.125 |
Tenga en cuenta que las probabilidades en la derecha; la columna se suman a 1. Las probabilidades totales para cualquier experimento debe ser siempre igual a 1.
El PDF para variables aleatorias continuas
Si usted está observando una variable aleatoria continua, el PDF se puede describir en una función o un gráfico. La función muestra cómo se comporta la variable aleatoria a través de cualquier rango posible de valores. En una representación gráfica de la PDF, los posibles valores de la variable aleatoria están en el eje horizontal, y una curva (sin ningún tipo de barras o roturas) está en algún lugar por encima del eje.
El PDF continua más común es la de una variable aleatoria distribuida normalmente. La representación gráfica de este PDF se muestra aquí.
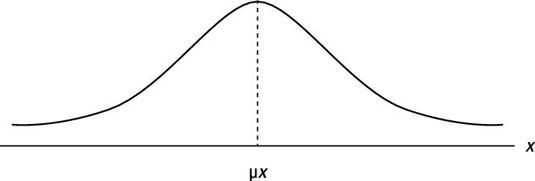
Independientemente de los valores de la media y la desviación estándar, la densidad total (área) bajo la curva es igual a 1. Además, alrededor del 68 por ciento de la densidad está dentro de una desviación estándar, aproximadamente el 95 por ciento de la densidad está dentro de estándar de dos desviaciones, y alrededor de 99,7 por ciento de la densidad está dentro de tres desviaciones estándar.
Debido a que una variable aleatoria continua puede tomar infinitos valores, la probabilidad de que se produzca un valor específico es cero!
Un ejemplo puede ayudar a ilustrar este punto. Supongamos que un profesor elige al azar uno de sus estudiantes econometría. ¿Cuál es la probabilidad de que el estudiante será exactamente 21 años de edad? Respuesta: esencialmente cero.
La razón es que el estudiante tendría que ser seleccionados al azar en el preciso día, horas, minutos, segundos y fracciones de segundo que él o ella nació hace 21 años. Eso sería prácticamente imposible. Habría, sin embargo, alguna posibilidad de seleccionar al azar un estudiante que está entre las edades de 20 y 22.
Probabilidades con variables aleatorias continuas se miden en intervalos. Matemáticamente, esta medición se expresa como probabilidad
dónde Xla y Xb son posibles valores que pueden ser adoptadas por la variable aleatoria X.
-
Bivariado o probabilidad conjunta densidad y la econometría -
Econometría y la función de densidad acumulativa (CDF) -
Cómo hacer generalizaciones en la econometría con valor esperado o media -
Cómo predecir el futuro con la densidad de probabilidad condicional -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal
La determinación de la media de una variable aleatoria discreta Cuando se trabaja con variables aleatorias, debe ser capaz de calcular e interpretar la media. Para estos problemas, y mucho X ser el número de clases tomadas por un estudiante universitario en un semestre. Utilice la fórmula para la media de una…
Diferenciar entre distribuciones de probabilidad discretas y continuas LA Distribución de probabilidad es una fórmula o una tabla utilizada para asignar probabilidades a cada posible valor de una variable aleatoria X. Una distribución de probabilidad puede ser o bien discreto o continua. Una distribución discreta…
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
Cómo calcular las probabilidades geométricas La distribución geométrica se basa en el proceso binomial (una serie de ensayos independientes con dos resultados posibles). Se utiliza la distribución geométrica para determinar la probabilidad de que un determinado número de pruebas se…
Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…
¿Cómo definir una variable estadística aleatoria En estadística, un variable al azar es una característica, medida o recuento que cambia aleatoriamente de acuerdo con un determinado conjunto o patrón. Variables aleatorias son generalmente denotan con letras mayúsculas como X, Y, Z,…
Cómo identificar una variable aleatoria binomial La variable aleatoria discreta más conocido y amado en las estadísticas es el binomio. Binomial medio dos nombres y se asocia con situaciones que participen dos resultados- por ejemplo, sí / no, o el éxito / fracaso (golpear una luz roja o no,…
Cómo identificar una distribución muestral En estadística, una distribución de muestreo se basa en promedios de la muestra en lugar de los resultados individuales. Esto hace que sea diferente de una distribución. He aquí por qué: A variable al azar es una característica de interés que…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
Cómo indicar posibles resultados de una variable aleatoria discreta Una variable aleatoria discreta X puede tomar en un determinado conjunto de resultados posibles, y cada uno de esos resultados tiene una cierta probabilidad estadística de que se produzcan. La notación utilizada para cualquier resultado…
Cómo utilizar el operador de suma para calcular el valor esperado Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…