Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central
Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces la media de la muestra es una variable aleatoria distribuida normalmente. Para determinar las probabilidades de la media de la muestra
las tablas normales estándar que usted requiere para convertir
a una variable aleatoria normal estándar.
La distribución normal estándar es el caso especial donde la media
es igual a 0, y la desviación estándar
es igual a 1.
Para cualquier variable aleatoria normalmente distribuida X con una media
y una desviación estándar
a encontrar la variable aleatoria normal estándar correspondiente (Z) Con la siguiente ecuación:
Para la distribución muestral de
la ecuación correspondiente es
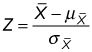
A modo de ejemplo, dicen que hay 10.000 existencias comerciales cada día en una bolsa de valores regional. Se sabe de la experiencia histórica de que los rendimientos de estas acciones tienen un valor promedio de 10 por ciento anual, y una desviación estándar de 20 por ciento anual.
Un inversionista opta por comprar una selección aleatoria de 100 de estas poblaciones por su cartera. ¿Cuál es la probabilidad de que la tasa media de rentabilidad entre estas 100 acciones es mayor que el 8 por ciento?
La cartera de la inversionista puede ser pensado como una muestra de las acciones elegidas por la población de existencias comerciales en el intercambio regional. El primer paso para encontrar esta probabilidad es calcular los momentos de la distribución muestral.
Calcule la media:
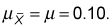
La media de la distribución muestral es igual a la media de la población.
Determinar el error estándar: Este cálculo es un poco más difícil debido a que el error estándar depende del tamaño de la muestra en relación con el tamaño de la población. En este caso, el tamaño de la muestra (n) Es de 100, mientras que el tamaño de la población (N) Es 10.000. Así que primero hay que calcular el tamaño de la muestra en relación con el tamaño de la población, así:
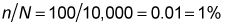
Debido a que el 1 por ciento es inferior al 5 por ciento, no se utiliza el factor de corrección de la población finita para calcular el error estándar. Tenga en cuenta que en este caso, el valor del factor de corrección población finita es:
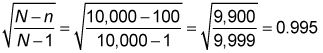
Debido a que este valor es tan cerca de 1, utilizando el factor de corrección de la población finita en este caso tendría poco o ningún impacto sobre las probabilidades resultantes.
Y debido a que el factor de corrección de población finita no es necesario en este caso, el error estándar se calcula como sigue:
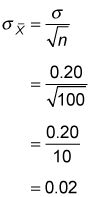
Para determinar la probabilidad de que la media de la muestra es mayor que el 8 por ciento, ahora debe convertir la media de la muestra en una variable aleatoria normal estándar utilizando la siguiente ecuación:
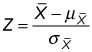
Para calcular la probabilidad de que la media de la muestra es mayor que 8 por ciento, de aplicar la fórmula anterior como sigue:
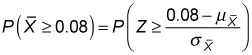
Porque
estos valores se sustituyen en la expresión anterior como sigue:
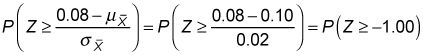
Se puede calcular esta probabilidad mediante el uso de las propiedades de la distribución normal estándar, junto con una tabla normal estándar como este.
| Z | 0.00 | 0.01 | 0.02 | 0.03 |
|---|---|---|---|---|
| -1.3 | 0.0968 | 0.0951 | 0.0934 | 0.0918 |
| -1.2 | 0.1151 | 0.1131 | 0.1112 | 0.1093 |
| -1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 |
| -1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 |
La tabla muestra la probabilidad de que una variable aleatoria normal estándar (designado Z) es Menos que o igual a un valor específico. Por ejemplo, puede escribir la probabilidad de que
(una desviación estándar por debajo de la media), como
Usted encuentra que la probabilidad de la mesa con los siguientes pasos:
Busque el primer dígito antes y después del punto decimal (-1,0) en el primero (Z) Columna.
Encuentra el segundo dígito después del punto decimal (0.00) en el segundo (0.00) la columna.
Ver en la fila y la columna se cruzan para encontrar la probabilidad:
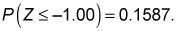
Debido a que en realidad estás en busca de la probabilidad de que Z es mayor que o igual a -1, se requiere un paso más.
Debido a la simetría de la distribución normal estándar, la probabilidad de que Z es mayor que o igual a un valor negativo es igual a uno menos la probabilidad de que Z es menor que o igual a el mismo valor negativo.
Por ejemplo,
Esto es porque
son complementario eventos. Esto significa eso Z o bien debe ser mayor que o igual a -2 o menor que o igual a -2. Por Consiguiente,
Esto es cierto porque la ocurrencia de uno de estos eventos es cierto, y la probabilidad de un evento determinado es 1.
Después de volver a escribir esta ecuación algebraica, usted termina con el siguiente resultado:
Para el ejemplo de la cartera,
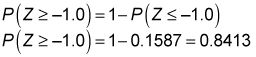
El resultado muestra que hay una probabilidad de 84.13 por ciento de que la cartera del inversor tendrá una media retorno superior al 8 por ciento.






