Cómo probar una hipótesis para la media de un población

Usted puede utilizar una prueba de hipótesis para examinar o impugnar una reclamación estadística sobre una media poblacional si la variable es numérica (por ejemplo, edad, ingresos, tiempo, etc.) y sólo una población o grupo (como todos los hogares o la totalidad estudiantes universitarios) se está estudiando. Por ejemplo, un psicólogo infantil, dice que el promedio de tiempo que las madres trabajadoras pasan a hablar con sus hijos es de 11 minutos por día, en promedio. La variable - el tiempo - es numérica, y la población es a todas las madres que trabajan. Usando la notación estadístico,

representa el número promedio de minutos por día que todas las madres que trabajan pasan hablando con sus hijos, en promedio.

La hipótesis nula es que la media poblacional,

es igual a un cierto valor reivindicada,

La notación para la hipótesis nula es

Así que la hipótesis nula en este ejemplo es

Las tres posibilidades para la hipótesis alternativa, H_la, son

dependiendo de lo que usted está tratando de mostrar.

Si usted sospecha que el tiempo promedio de las madres que trabajan pasan hablando con sus hijos es más de 11 minutos, su hipótesis alternativa sería

Para probar la reclamación, se compara la media que obtuvo de su muestra

con la media se muestra en H₀

Para hacer una comparación adecuada, nos fijamos en la diferencia entre ellos, y se divide por el error estándar de tener en cuenta el hecho de que sus resultados de la muestra pueden variar. Este resultado es su estadística de prueba. En el caso de una prueba de hipótesis para la media de la población, la estadística de prueba resulta (bajo ciertas condiciones) para ser un zvalor (un valor de la Z-distribución).

A continuación, puede buscar su estadística de prueba en la tabla correspondiente (en este caso, se mira para arriba en el siguiente Z-tabla), y encontrar la probabilidad de que resulte más extremas que las que se encuentran en la muestra se podría haber encontrado. Normalmente, si el estadístico de prueba Z es positivo, usted quiere encontrar la probabilidad de que Z es mayor que la estadística de prueba. Si prueba estadística es negativa, usted quiere encontrar la probabilidad de que Z es menor que el estadístico de prueba.

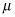
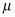
La estadística de prueba para probar un solo media poblacional (bajo ciertas condiciones) es

para este caso que se conoce este número), y n es el tamaño de la muestra. Para el cálculo de la estadística de prueba, haga lo siguiente:

1. Calcular la media de la muestra,

   

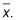
2. Encontrar

   

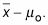
3. Calcule el error estándar:

   

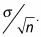
4. Divida el resultado del paso 2 por el error estándar que se encuentra en el paso 3.

Las condiciones para el uso de esta estadística de prueba es que la desviación estándar de la población,

es conocido, y, o bien la población tiene una distribución normal o el tamaño de la muestra es lo suficientemente grande como para utilizar el teorema del límite central (n > 30).

Para este ejemplo, supongamos que una muestra aleatoria de 100 madres trabajadoras pasan un promedio de 11,5 minutos al día hablando con sus hijos. Asumir la investigación previa sugiere la desviación estándar de la población es de 2,3 minutos.

1. Se le da que

   

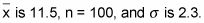
2. Tome 11,5-11 = 0,5.

3. Tomar 2,3 dividido por la raíz cuadrada de 100 (que es 10) para obtener 0,23 para el error estándar.

4. Divide +0,5 por 0.23 para obtener 2.17. Esa es su estadística de prueba, lo que significa que su media de la muestra es de 2,17 errores estándar por encima de la población reclamado significan.

La gran idea de una prueba de hipótesis es desafiar la afirmación de que se está realizando sobre la población (en este caso, la media poblacional) - esa afirmación se muestra en la hipótesis nula, H₀. Si usted tiene suficiente evidencia de su muestra en contra de la reclamación, H₀ se rechaza.

Para decidir si tiene suficiente evidencia para rechazar H₀, calcular el p-valor por buscar su estadística de prueba (en este caso 2.17) en la normal estándar (Z-) Distribución - ver lo anterior Z-mesa - y tomar 1 menos la probabilidad muestra. (Usted restar de 1 porque su H_la es una mayor que la hipótesis y la tabla muestra menos que las probabilidades.)

Para este ejemplo se mira la estadística de prueba (2.17) en la Z-mesa y encontrar la probabilidad (menor que) es 0.9850, por lo que el p-valor es 1 a 0,9850 = 0,015. Es un poco menos de su nivel (típico) significancia de 0.05, lo que significa que sus resultados de la muestra son bastante estadísticamente significativa. Así rechazar la reclamación

Sus resultados apoyan la hipótesis alternativa

Según sus datos, la afirmación del psicólogo infantil de 11 minutos por día es demasiado baja el promedio real es mayor que eso.

La tentación es decir: "Bueno, yo sabía que la reclamación de 11 minutos por día era demasiado bajo porque la media de la muestra de 11,5 minutos era claramente más grande. ¿Por qué me necesito una prueba de hipótesis?" Todo ese número te dice algo acerca de esos 100 madres de la muestra. También es necesario tener en cuenta la variación utilizando el error estándar y la distribución normal para poder decir algo acerca de toda la población de las madres trabajadoras.