Cómo probar una hipótesis nula basada en una proporción de la población

Usted puede utilizar una prueba de hipótesis para probar un reclamo estadística sobre una proporción de la población cuando la variable es categórica (por ejemplo, el género o el apoyo / oposición) y está en estudio una sola población o grupo (por ejemplo, todos los votantes registrados).

La prueba analiza la proporción (p) De los individuos de la población que tienen una determinada característica - por ejemplo, la proporción de personas que portan teléfonos celulares. La hipótesis nula es H₀: p = p₀, dónde p₀ es un cierto valor reclamado de la proporción de la población, p. Por ejemplo, si la demanda es que el 70% de las personas llevar a los teléfonos celulares, p₀ es 0,70. La hipótesis alternativa es uno de los siguientes:

La fórmula para la estadística de prueba para una sola proporción (bajo ciertas condiciones) es:

y z es un valor en el Z-distribución. Para el cálculo de la estadística de prueba, haga lo siguiente:

1. Calcular la proporción de la muestra,

   

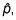
   tomando el número de personas de la muestra que tienen la característica de interés (por ejemplo, el número de personas de la muestra que lleva teléfonos móviles) y dividiendo esa por n, el tamaño de la muestra.

2. Encontrar

   

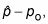
   dónde p_o es el valor en H_o.

3. Calcule el error estándar,

   

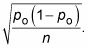
4. Divida el resultado del paso 2 por el resultado del paso 3.

Para interpretar la estadística de prueba, busque su estadística de prueba en la normal estándar (Z-) Y calcular la distribución p-valor.

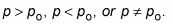
Las condiciones para el uso de esta estadística de prueba son que

Por ejemplo, supongamos que Cavifree afirma que cuatro de cada cinco dentistas recomiendan Cavifree pasta dental a sus pacientes. En este caso, la población es todos los dentistas, y p es la proporción de todos los dentistas que recomendaron Cavifree. La pretensión es que p es igual a "cuatro de cada cinco", o p₀ 4 está dividido por 5 = 0,80. Sospecha que la proporción es en realidad menos de 0,80. Sus hipótesis son H₀: p = 0,80 frente a H_la: p lt; 0.80.

Supongamos que 151 fuera de su muestra de 200 pacientes dentales reportaron haber recibido una recomendación para Cavifree de su dentista. Para encontrar la estadística de prueba para estos resultados, siga estos pasos:

1. Empezar con

   

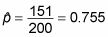
   y n = 200.

2. Porque p_o = 0,80, p tomar (sombrero) -p₀= 0,755 hasta 0,80 = -0,045 como numerador del estadístico de prueba.

3. A continuación, es igual al error estándar

   

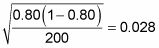
   (el denominador de la estadística de prueba).

4. La estadística de prueba es

   

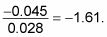
Debido a que la prueba estadística resultante es negativo, significa que los resultados de las muestras son -1.61 errores estándar por debajo (menos de) el valor reclamado para la población. ¿Con qué frecuencia se puede esperar para obtener resultados como éste si H₀ fuera cierto? La oportunidad de estar en o más allá (en este caso menos) -1,61 es 0.0537. (Mantenga la negativa con el número y buscar -1,61 en el anterior Z-mesa.) Este resultado es su p-valor, porque H_la es un menos-que-hipótesis.

Porque el p-valor sea superior a 0,05 (aunque no por mucho), no tiene más que suficiente evidencia para rechazar H₀. Usted concluye que la afirmación de que el 80% de los dentistas recomiendan Cavifree no puede ser rechazada, de acuerdo con sus datos. Sin embargo, es importante reportar el actual p-valorar también, para que otros puedan tomar sus propias decisiones.

Usted podría preguntarse, "Hey, la proporción muestral de 0.755 es mucho menor que la proporción reclamada de 0.80. ¿Por qué la prueba de hipótesis rechazar H₀ desde 0.755 es menor que 0,80? "Porque en este caso, 0.755 no es significativamente menor que 0,80. También es necesario tener en cuenta la variación utilizando el error estándar y la distribución normal para poder decir algo acerca de toda la población de los dentistas.

La carta p se utiliza de dos maneras diferentes en este ejemplo: p-valor y p. La carta p por sí mismo indica la proporción de la población, no el p-valor. No se confunda. Cada vez que se reporta un p-valor, asegúrese de agregar -valor así que no es confundida con p, la proporción de población.