Cómo comparar dos medias poblacionales independientes

Puede comparar los datos numéricos de dos poblaciones o grupos (como los niveles de colesterol en los hombres frente a las mujeres, o los niveles de ingreso de la escuela secundaria en comparación con los graduados universitarios) estadísticos para probar una afirmación acerca de la diferencia en los promedios. (Por ejemplo, es la diferencia en la población significa igual a cero, lo que indica sus medios son iguales?) Dos (totalmente separadas) muestras aleatorias independientes deben ser seleccionados, uno de cada población, a fin de recopilar los datos necesarios para esta prueba .

La hipótesis nula es que las dos medias de población son el mismo: en otras palabras, que su diferencia es igual a 0. La notación para la hipótesis nula es

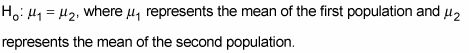
También puede escribir la hipótesis nula como

haciendo hincapié en la idea de que su diferencia es igual a cero si los medios son los mismos.

La fórmula de la estadística de prueba se comparan dos medios (bajo ciertas condiciones) es:

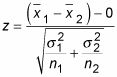
Para calcularlo, haga lo siguiente:

1. Calcular las medias de la muestra

   

   se les da.) Vamos n₁ y n₂ representar los dos tamaños de muestra (no necesitan ser iguales).

2. Encuentra la diferencia entre las dos medias de la muestra:

   

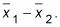
   Tenga en cuenta que debido a que

   

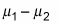
   es igual a 0 si H₀ Es cierto, no es necesario que se incluirán en el numerador de la estadística de prueba. Sin embargo, si la diferencia de que están poniendo a prueba es un valor distinto de 0, se resta ese valor de x₁-X₂ en el numerador de la estadística de prueba.

3. Calcular el error estándar utilizando la siguiente ecuación:

   

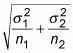
4. Divida el resultado del paso 2 por el resultado del paso 3.

   Para interpretar la estadística de prueba, añadir los dos pasos siguientes en la lista:

5. Busque su estadística de prueba en la normal estándar (Z-) Distribución (ver el siguiente Z-tabla) y calcular el p-valor.

   

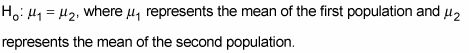
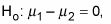
6. Compare el p-valor a su nivel de significación, (como 0.05). Si es menor o igual a tu nivel de significación, rechazar H₀. De lo contrario, dejar de rechazar H₀.

Las condiciones para el uso de esta prueba son que las dos desviaciones estándar poblacionales son conocidos y, o bien ambas poblaciones tienen una distribución normal o ambos tamaños de las muestras son lo suficientemente grandes para el teorema del límite central a aplicar.

Por ejemplo, suponga que desea comparar la capacidad de absorción de dos marcas de toallas de papel (llamar a las marcas Estadísticas absorbentes y esponja-o-matic). Usted puede hacer esta comparación por mirar el número medio de onzas cada marca puede absorber antes de ser saturado. H₀ dice que la diferencia entre las absorbancias promedio es de 0 (inexistente), y H_la dice que la diferencia no es 0. En otras palabras, una marca es más absorbente que el otro. Utilizando la notación estadística, usted tiene

Aquí, usted no tiene ninguna indicación de que la toalla de papel puede ser más absorbente, por lo que la no-igual alternativa es la de utilizar.

Suponga que se selecciona una muestra aleatoria de 50 toallas de papel de cada marca y medir la capacidad de absorción de cada toalla de papel. Supongamos que la capacidad de absorción media de Estadísticas absorbente (X₁) Para su muestra es de 3 onzas, y asumen la desviación estándar de la población es de 0,9 oz. Para Sponge-o-matic (X₂), La absorbencia promedio es de 3,5 oz de acuerdo a sus muestra- asumen la desviación estándar de la población es de 1,2 oz. Llevar a cabo esta prueba de hipótesis siguiendo los 6 pasos anteriores:

1. Teniendo en cuenta la información anterior, ya sabes

   

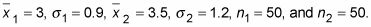
2. La diferencia entre las medias muestrales para (Estadísticas absorbente - Sponge-o-matic) es

   

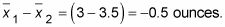
   (A diferencia negativa simplemente significa que la segunda media de la muestra fue mayor que el primero.)

3. El error estándar es

   

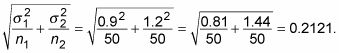
4. Divida la diferencia, -0,5, por el error estándar, 0,2121, lo que le da -2.36. Esta es su estadística de prueba.

5. Para encontrar la p-valor, mirar hacia arriba -2,36 en la normal estándar (Z-) Distribución - ver lo anterior Z-mesa. La oportunidad de estar allá, en este caso a la izquierda de, -2.36 es igual a 0,0091. Debido H_la es un-no-igual a alternativa, el doble de este porcentaje para obtener 2 # 8727- 0,0091 = 0,0182, su p-valor.

6. Esta p-valor es un poco menos de 0,05. Eso significa que tiene evidencia bastante fuerte para rechazar H₀.

Su conclusión es que existe una diferencia estadísticamente significativa entre los niveles de absorción de estas dos marcas de toallas de papel, basado en sus muestras. Y Esponja-o-matic que sale en la parte superior, ya que tiene un promedio más alto. (Estadísticas-absorbentes menos Sponge-o-matic negativo significa ser Sponge-o-matic tuvo el valor más alto.)

La tentación es decir, " Bueno, yo sabía que la afirmación de que los niveles de absorción son iguales que estaba mal porque una marca tenía una media muestral de 3.5 onzas, y el otro fue de 3,0 onzas. ¿Por qué aún necesito una prueba de hipótesis "? Todos esos números te dicen es algo acerca de esos 100 toallas de papel de muestra. También es necesario tener en cuenta la variación utilizando el error estándar y la distribución normal para poder decir algo acerca de toda la población de toallas de papel.