Calcular estadísticas de prueba para dos poblaciones independientes con varianzas desiguales y al menos una pequeña muestra
Si las varianzas de dos poblaciones independientes aren't igual (o usted no tiene ninguna razón para creer que son iguales) y al menos una muestra es pequeño (menos de 30), la prueba estadística apropiada es
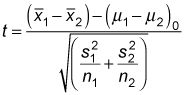
En este caso, se obtiene los valores críticos de la distribución t con grados de libertad (df) igual a
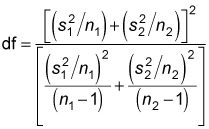
Tenga en cuenta que este valor no es necesariamente igual a todo un número- si el valor resultante contiene una parte fraccional, debe redondear al siguiente número entero más cercano.
Por ejemplo, supongamos que la Major League Baseball (MLB) está interesado en determinar si la media del número de carreras anotadas por juego es más alta en la Liga Americana (AL) que en la Liga Nacional (Liga Nacional). Las variaciones de población se supone que son desiguales.
El primer paso es asignar un grupo a representar a la primera población ("población 1") y el otro grupo para representar a la segunda población ("población 2"). MLB designa la Liga Americana como la población 1 y la Liga Nacional como la población 2.
El siguiente paso es elegir las muestras de ambas poblaciones. Supongamos que MLB elige una muestra de 10 de la Liga Americana y 12 equipos de la Liga Nacional. Los resultados se utilizan para calcular la media de la muestra y muestra la desviación estándar para ambas ligas. Supongamos que la media de la muestra de carreras anotadas entre los juegos de la Liga Americana es de 8.1, mientras que la media de la muestra para los juegos de la Liga Nacional es de 7.9. La desviación estándar de la muestra es de 0,5 para los juegos de la Liga Americana y 0.3 para los juegos de la Liga Nacional.
MLB pone a prueba la hipótesis nula de que la población puntuaciones medias son iguales al nivel del 5 por ciento de significancia.
He aquí un resumen de los datos de ejemplo:
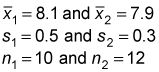
La hipótesis nula es
Debido a que la MLB está interesado en determinar si la media del número de carreras anotadas por juego es más alta en la Liga Americana que en la Liga Nacional, se utiliza un derecho; prueba de cola. La hipótesis alternativa es
En otras palabras, la prueba está diseñado para encontrar una fuerte evidencia de que la media de la población es 1 mayor de la media de la población 2. A continuación, resolver la estadística de prueba de la siguiente manera:
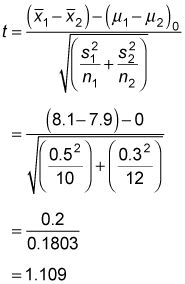
Y a encontrar los grados de libertad, así:
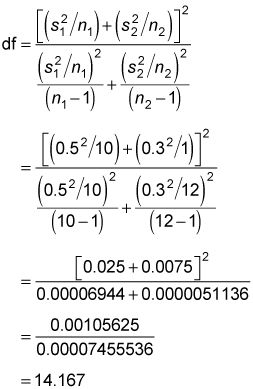
Usted redondear a la baja el valor de 14,167 a 14 debido a que los grados de libertad debe ser un número entero (o entero). Con 14 grados de libertad y un nivel de significación del 5 por ciento, el valor crítico es
Este resultado se obtiene a partir de la siguiente tabla mediante la búsqueda de la columna encabezada t0.05 y la fila correspondiente a 14 grados de libertad.
| Grados de libertad | t0.10 | t0.05 | t0,025 | t0.01 | t0,005 |
|---|---|---|---|---|---|
| 6 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 |
| 10 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
| 11 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 |
| 12 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 |
| 13 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 |
| 14 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 |
| 15 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 |
Debido a que la estadística de prueba (1.109) está por debajo del valor crítico (1.761), la hipótesis nula de que
deja de ser rechazada. No hay pruebas suficientes para concluir que más carreras se anotan durante los partidos de la Liga Americana que los juegos de la Liga Nacional.
-
Pruebas de hipótesis para los valores extremos de datos -
Análisis exploratorio de datos cuantitativos (eda) técnicas -
Cómo utilizar todos, algunos, y cualquier en sentencias SQL - 10 Conceptos clave en la prueba de hipótesis
-
Calcular las pruebas estadísticas apropiadas para dos poblaciones grandes, independientes con varianzas desiguales - Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis
La evaluación de reclamaciones con pruebas de hipótesis Utiliza las pruebas de hipótesis para desafiar si alguna afirmación sobre una población es cierto (por ejemplo, la afirmación de que el 90 por ciento de los estadounidenses posee un teléfono celular). Para poner a prueba una hipótesis…
Explora prueba de hipótesis en las estadísticas comerciales En estadística, hprueba ypothesis se refiere al proceso de elegir entre hipótesis opuestas sobre una distribución de probabilidad, basándose en los datos observados a partir de la distribución. Es un tema central y una parte fundamental del…
Encuentra las pruebas estadísticas apropiadas para dos poblaciones independientes de igual tamaño y varianza Puede probar hipótesis acerca de dos medias poblacionales donde las poblaciones son independientes entre sí, pero tienen el mismo tamaño y la varianza. Con igual varianzas poblacionales, la estadística de prueba requiere el cálculo de una…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una pequeña muestra Cuando se utiliza una pequeña muestra para probar una hipótesis acerca de una media poblacional, se toma el valor crítico resultante o los valores de la distribución t de Student. Para una prueba de dos colas, el valor crítico esy n representa…
Cómo comparar dos medias poblacionales independientes Puede comparar los datos numéricos de dos poblaciones o grupos (como los niveles de colesterol en los hombres frente a las mujeres, o los niveles de ingreso de la escuela secundaria en comparación con los graduados universitarios) estadísticos…
Cómo determinar un valor de p al probar una hipótesis nula Al probar una hipótesis sobre una población, puede utilizar el estadístico de prueba para decidir si se debe rechazar la hipótesis nula, H0. A tomar esta decisión mediante la presentación de un número, llamado p-valor.LA p-valor es una…
¿Cómo encontrar los valores críticos para una hipótesis de ANOVA utilizando el f-mesa Usted puede encontrar los valores críticos para una hipótesis de ANOVA utilizando la mesa F. Debido a que la distribución F se basa en dos tipos de grados de libertad, hay una tabla para cada posible valor de alfa (el nivel de significación).La…
¿Cómo encontrar t *-valores para los intervalos de confianza Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
Cómo probar una hipótesis para la media de un población Usted puede utilizar una prueba de hipótesis para examinar o impugnar una reclamación estadística sobre una media poblacional si la variable es numérica (por ejemplo, edad, ingresos, tiempo, etc.) y sólo una población o grupo (como todos los…
Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos Cuando se utiliza una prueba estadística para una media poblacional, hay dos casos en los que debe utilizar el t-distribución en lugar de la Z-distribución. El primer caso es donde el tamaño de la muestra es pequeño (por debajo de 30 o así), y…
Visión general de la prueba de hipótesis Una forma importante para sacar conclusiones acerca de las propiedades de una población es con la prueba de hipótesis. Puedes usar pruebas de hipótesis para comparar una medida de población a un valor especificado, comparar las medidas para dos…