Calcular las pruebas estadísticas apropiadas para dos poblaciones grandes, independientes con varianzas desiguales
Cuando usted está poniendo a prueba hipótesis sobre dos medias de población, donde las varianzas de las dos poblaciones no son iguales, y el tamaño de ambas muestras son grandes (30 o más), la prueba estadística apropiada es
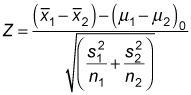
Esta estadística prueba se basa en la distribución normal estándar.
A modo de ejemplo, digamos que una cadena de restaurantes está interesado en saber si la venta promedio por cliente es el mismo en sus restaurantes nacionales y extranjeros. Las variaciones de población se supone que son desiguales. El restaurante elige una muestra aleatoria de 40 nacionales y 50 restaurantes extranjeros, la designación de restaurantes nacionales como la población 1 y restaurantes extranjeros como la población 2.
La media de la muestra el gasto por cliente es de $ 5,14 en el mercado nacional y $ 4,59 en el mercado externo. La desviación estándar de la muestra es de $ 0,54 en el mercado nacional y $ 0,38 en el mercado externo. La hipótesis nula de que la media de la población el gasto es igual en los dos mercados se prueba al nivel del 5 por ciento de significancia.
He aquí un resumen de estos datos:
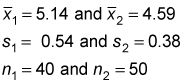
La hipótesis nula es
Debido a que este ejemplo se requiere una prueba de dos colas, la hipótesis alternativa es
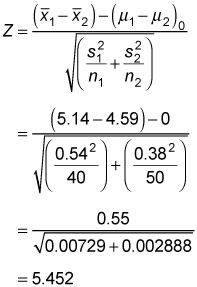
Usted encontrará la estadística de prueba de este modo:
Ahora se utiliza la tabla normal estándar para encontrar los valores críticos.
| Z | 0.04 | 0.05 | 0.06 | 0.07 |
|---|---|---|---|---|
| 15 | 0.9382 | 0.9394 | 0.9406 | 0.9418 |
| 16 | 0.9495 | 0.9505 | 0.9515 | 0.9525 |
| 1.7 | 0.9591 | 0.9599 | 0.9608 | 0.9616 |
| 1.8 | 0.9671 | 0.9678 | 0.9686 | 0.9693 |
| 1.9 | 0.9738 | 0.9744 | 0.9750 | 0.9756 |
| 2.0 | 0.9793 | 0.9798 | 0.9803 | 0.9808 |
A partir de la tabla, a encontrar los valores críticos para ser
Debido a que la estadística de prueba (5.452) es mayor que el valor positivo crítico (1.96), la hipótesis nula
se rechaza.
Debido a que esta es una prueba de dos colas, puede rechazar la hipótesis nula a favor de la alternativa
(es decir, la media de gasto por cliente es mayor en el mercado interno que el mercado externo) o
(es decir, la media de gasto por cliente es más bajo en el mercado interno que el mercado extranjero.) Debido a que la estadística de prueba es grande y positiva, la alternativa
se elige. En otras palabras, significa que el gasto por cliente en el mercado nacional es mayor que en el mercado externo.
-
Pruebas de hipótesis para los valores extremos de datos -
Análisis exploratorio de datos cuantitativos (eda) técnicas -
10 Conceptos clave en la prueba de hipótesis - La aplicación de la prueba de hipótesis en las estadísticas comerciales
-
Calcular estadísticas de prueba para dos poblaciones independientes con varianzas desiguales y al menos una pequeña muestra - Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis
La evaluación de reclamaciones con pruebas de hipótesis Utiliza las pruebas de hipótesis para desafiar si alguna afirmación sobre una población es cierto (por ejemplo, la afirmación de que el 90 por ciento de los estadounidenses posee un teléfono celular). Para poner a prueba una hipótesis…
Explora prueba de hipótesis en las estadísticas comerciales En estadística, hprueba ypothesis se refiere al proceso de elegir entre hipótesis opuestas sobre una distribución de probabilidad, basándose en los datos observados a partir de la distribución. Es un tema central y una parte fundamental del…
Encuentra las pruebas estadísticas apropiadas para dos poblaciones independientes de igual tamaño y varianza Puede probar hipótesis acerca de dos medias poblacionales donde las poblaciones son independientes entre sí, pero tienen el mismo tamaño y la varianza. Con igual varianzas poblacionales, la estadística de prueba requiere el cálculo de una…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una pequeña muestra Cuando se utiliza una pequeña muestra para probar una hipótesis acerca de una media poblacional, se toma el valor crítico resultante o los valores de la distribución t de Student. Para una prueba de dos colas, el valor crítico esy n representa…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande En estadística, una amplia muestra tiene un tamaño mayor o igual a 30. Cuando se utiliza una gran muestra para probar una hipótesis acerca de una media poblacional, el valor o valores críticos resultante de dos colas de la distribución normal…
Manejo de pruebas de hipótesis estadísticas Utiliza las pruebas de hipótesis para desafiar si alguna afirmación sobre una población es cierto (por ejemplo, la afirmación de que el 40 por ciento de los estadounidenses posee un teléfono celular). Para poner a prueba una hipótesis…
Cómo comparar dos medias poblacionales independientes Puede comparar los datos numéricos de dos poblaciones o grupos (como los niveles de colesterol en los hombres frente a las mujeres, o los niveles de ingreso de la escuela secundaria en comparación con los graduados universitarios) estadísticos…
Cómo determinar un valor de p al probar una hipótesis nula Al probar una hipótesis sobre una población, puede utilizar el estadístico de prueba para decidir si se debe rechazar la hipótesis nula, H0. A tomar esta decisión mediante la presentación de un número, llamado p-valor.LA p-valor es una…
Cómo configurar una prueba de hipótesis: null frente alternativa Al configurar una prueba de hipótesis para determinar la validez de una afirmación estadística, es necesario definir tanto una hipótesis nula y la hipótesis alternativa.Normalmente, en una prueba de hipótesis, la reclamación se están…
Cómo probar una hipótesis para la media de un población Usted puede utilizar una prueba de hipótesis para examinar o impugnar una reclamación estadística sobre una media poblacional si la variable es numérica (por ejemplo, edad, ingresos, tiempo, etc.) y sólo una población o grupo (como todos los…
Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos Cuando se utiliza una prueba estadística para una media poblacional, hay dos casos en los que debe utilizar el t-distribución en lugar de la Z-distribución. El primer caso es donde el tamaño de la muestra es pequeño (por debajo de 30 o así), y…
En cuanto a los valores críticos del intervalo de confianza Los valores críticos (z*-valores) son un componente importante de los intervalos de confianza (la técnica estadística para estimar parámetros poblacionales). los z* -valor, que aparece en el margen de la fórmula de error, mide el número de…