Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos

Cuando se utiliza una prueba estadística para una media poblacional, hay dos casos en los que debe utilizar el t-distribución en lugar de la Z-distribución. El primer caso es donde el tamaño de la muestra es pequeño (por debajo de 30 o así), y el segundo caso es cuando la desviación estándar de la población,

no se sabe, y usted tiene que estimar usando la desviación estándar de la muestra, s. En ambos casos, usted tiene menos información fiable sobre la que basar sus conclusiones, por lo que tiene que pagar una multa para esta utilizando el t-distribución, que tiene más variabilidad en las colas que una Z-distribución tiene.

Una prueba de hipótesis para una media poblacional que implica la t-distribución se llama t-prueba. La fórmula de la estadística de la prueba en este caso es:

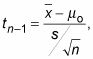
dónde t_n-1 es un valor de la t-de distribución con n-1 grados de libertad.

Tenga en cuenta que es igual que la estadística de prueba para la gran muestra y / o la caja de distribución normal, excepto

No se sabe, por lo que sustituye la desviación estándar de la muestra, s, en su lugar, y utilizar una t-valor en lugar de una z-valor.

Porque el t-distribución tiene colas más gordo que el Z-distribución, se obtiene una mayor p-valor de la t-distribución que uno que la normal estándar (Z-) Distribución te habría dado por la misma estadística de prueba. Un grande p-valor significa menos posibilidades de rechazar una hipótesis nula, H₀. Tener menos datos y / o no saber la desviación estándar de la población debe crear una mayor carga de la prueba.

Supongamos que una empresa de mensajería y afirma que entregar sus paquetes en 2 días en promedio, y sospecha que es más que eso. Las hipótesis son

Para probar esta afirmación, se toma una muestra aleatoria de 10 paquetes y grabar sus tiempos de entrega. Usted encuentra la media de la muestra es

y la desviación estándar de la muestra es de 0,35 días. (Debido a la desviación estándar de la población,

se desconoce, a estimar con s, la desviación estándar de la muestra.) Este es un trabajo para el t-prueba.

Debido a que el tamaño de la muestra es pequeño (n = 10 es mucho menor que 30) y la desviación estándar de la población no se conoce, su estadística de prueba tiene una t-distribución. Sus grados de libertad es 10-1 = 9. La fórmula de la estadística de prueba (denominado t-valor) es:

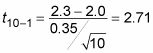
Para calcular el p-valor, nos fijamos en la fila en el t-mesa para df = 9.

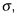
Su estadística de prueba (2.71) cae entre dos valores en la fila df = 9 en el t-tabla: 2,26 y 2,82 (redondeando a dos decimales). Para calcular el p-valor por su estadística de prueba, se encontró que las columnas corresponden a estos dos números. El número 2.26 aparece en la columna de 0.025 y el número 2.82 aparece en el 0.010 Columna ahora sabe la p-valor por su estadística de prueba se encuentra entre 0.025 y 0.010 (es decir, 0.010 lt; p-valor lt; 0,025).

Usando el t-mesa en la que no se conoce el número exacto para el p-valor, sino porque 0.010 y 0.025 son tanto menos de su nivel de significación de 0.05, se rechaza H₀- que tiene suficiente evidencia en su muestra de decir los paquetes no se están entregando en 2 días, y de hecho el tiempo de entrega promedio es de más de 2 días.

La tentación es decir, " Bueno, yo sabía que el reclamo de 2 días en promedio era demasiado bajo porque la media de la muestra de 2,3 minutos fue claramente mayor. ¿Por qué aún necesito una prueba de hipótesis "? Todo ese número te dice algo acerca de esos 10 paquetes de la muestra. También es necesario tener en cuenta la variación utilizando el error estándar y el t-distribución de poder decir algo sobre la población total de los paquetes enviados.

los t-tabla no incluye todos los posibles t-de valor simplemente encontrar los dos valores más cercanos a los suyos a ambos lados, mirar las columnas que están, y reportar su p-valor en relación a la de ellos. (Si el resultado es mayor que todo el t-valores de la fila correspondiente de la t-mesa, sólo tiene que utilizar el último uno su p-valor será menor que su probabilidad.)