¿Cómo encontrar los momentos de la distribución binomial
Momentos
Conteúdo
La varianza y la desviación estándar representan la dispersión entre los valores posibles de una distribución de probabilidad. La varianza y desviación estándar de una distribución de probabilidad son equivalentes a la varianza y la desviación estándar de una población o muestra. La varianza es a veces conocido como el segundo momento central de una probabilidad distribución- la desviación estándar no es un momento aparte, sino simplemente la raíz cuadrada de la varianza.
Por suerte, para la distribución binomial, puede reducir el tiempo de cálculo mediante el uso de una serie de fórmulas simplificadas.
Cómo calcular el valor esperado de la distribución binomial
los valor esperado de una distribución de probabilidad es su valor medio. Usted lo consigue pesando cada valor posible por su probabilidad de ocurrencia. Para la distribución binomial, el cálculo del valor esperado se puede simplificar a
E (x) = np
Por ejemplo, supongamos que el 10 por ciento de todas las personas que se quedan; entregó, y el 90 por ciento están en lo cierto; mano (que pasa a ser verdad). En una clase de 40 alumnos, ¿cuál es el número esperado de izquierda, estudiantes zurdos? Usted puede calcular el valor esperado por el pensamiento de cada estudiante como un "juicio", con una probabilidad del 10 por ciento de quedarse; mano (un "éxito") y el 90 por ciento de posibilidades de tener razón; mano (un "fracaso"). Por Consiguiente, n = 40 y p = 0.10. El número previsto de izquierda, los estudiantes entregaron en la clase es E (x) = np = (40) (0,10) = 4.
Cómo calcular la varianza y la desviación estándar de la distribución binomial
los desacuerdo de una distribución es la distancia al cuadrado media entre cada resultado posible y el valor esperado. Para la distribución binomial, es posible calcular la varianza con la siguiente fórmula simplificada:
los desviacion estandar de una distribución es igual a la raíz cuadrada de la varianza. Para la distribución binomial, se calcula la desviación estándar como
Para el ejemplo de la izquierda, estudiantes zurdos,
El valor esperado es E (X) = np = (40) (0,10) = 4.
La varianza es
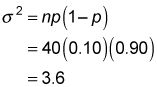
La desviación estándar es
-
Cómo hacer generalizaciones en la econometría con valor esperado o media -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal -
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t -
Cómo calcular la varianza y la desviación estándar en la distribución uniforme -
Cómo cambiar un valor de x para un valor z
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
Cómo utilizar el operador de suma para calcular el valor esperado Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
La desviación estándar, varianza, y el coeficiente de variación de los datos bioestadística los desviacion estandar (generalmente abreviado SD, sd, o solo s) De un montón de números te dice lo mucho que los números individuales tienden a ser diferentes (en cualquier dirección) de la media. Se calcula como sigue:Esta fórmula está…