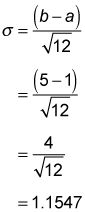Cómo calcular la varianza y la desviación estándar en la distribución uniforme
los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el "spread" entre los posibles valores de la distribución de probabilidad de una variable aleatoria.
Por ejemplo, supongamos que una galería de arte vende dos tipos de obras de arte: Impresiones de bajo costo y pinturas originales. La longitud de tiempo que las huellas permanecen en el inventario se distribuye uniformemente en el intervalo (0, 40). Por ejemplo, algunas impresiones se venden inmediato- sin letra permanece en el inventario por más de 40 días. Para las pinturas, la longitud de tiempo en el inventario se distribuye uniformemente en el intervalo (5, 105). Por ejemplo, cada cuadro requiere por lo menos 5 días para ser vendidos y puede tardar hasta 105 días para ser vendidos.
La varianza y la desviación estándar miden el grado de dispersión (spread) entre los valores de una distribución de probabilidad. En el ejemplo de la galería de arte, los tiempos de inventario de los grabados están mucho más cerca entre sí que para las pinturas. Como resultado, la varianza y la desviación estándar son mucho más bajos para las impresiones porque el rango de valores posibles es mucho menor.
Para la distribución uniforme definida sobre el intervalo desde la a b, la varianza es igual
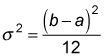
La desviación estándar es la raíz cuadrada de la varianza:
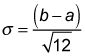
Por ejemplo, la varianza de la distribución uniforme definida sobre el intervalo (1, 5) se calcula como sigue:
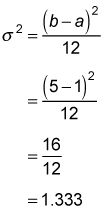
La desviación estándar es:
-
¿Cuánto propagación es allí en los datos? -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal -
La distribución chi-cuadrado en la econometría -
Cómo calcular la desviación estándar de un conjunto de datos estadísticos -
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
Cómo graficar la distribución uniforme los distribución uniforme es una distribución continua que asigna sólo probabilidades positivas dentro de un intervalo especificado (la, b) - Es decir, todos los valores entre la y b. (la y b son dos constants- pueden ser negativo o positivo.)Una…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
Distribuciones de probabilidad continuas Cuando se trabaja con distribuciones de probabilidad continuas, las funciones pueden tomar muchas formas. Estos incluyen uniforme continua, exponencial, normal, normal estándar (Z), la aproximación binomial, Poisson aproximación, y distribuciones…
La elección de la justa medida de dispersión en psicología estadística Las medidas de dispersión que utiliza en psicología estadística que muestran la dispersión o variabilidad de la variable que se está midiendo. Los tres principales son la gama, el rango intercuartil y la desviación estándar.Familiarización…