¿Cómo medir los momentos de la f-distribución

Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución F.

• los valor esperado que se conoce como el primer momento de una distribución de probabilidad y representa el valor medio o promedio de una distribución.

• los desacuerdo es el segundo momento central y muestra cómo se extienden o dispersos los valores de una distribución son en torno al valor esperado.

• los desviacion estandar No es un momento separado, pero es la raíz cuadrada de la varianza.

Para la mayoría de aplicaciones, la desviación estándar es más útil que la varianza (debido a la desviación estándar se mide en las mismas unidades que el valor esperado mientras que la varianza no lo es). Para la distribución F, se utiliza esta fórmula para determinar el valor esperado:

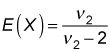
E(X) Representa el valor esperado, y

representa los grados de libertad del denominador.

La fórmula valor esperado requiere que los grados de libertad del denominador sea mayor que 2. De lo contrario, el valor esperado se vuelve negativa o indefinida.

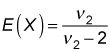
El valor esperado representa la promedio valor de la distribución F. Por ejemplo, esta cifra muestra un gráfico de la distribución F con 5 grados de libertad del numerador y 5 grados de libertad del denominador. El valor esperado es igual a:

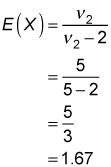
La figura también muestra un gráfico de la distribución F con 20 grados de libertad del numerador y 20 grados de libertad del denominador. El valor esperado es igual a:

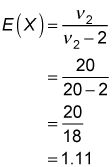
Esto demuestra que el valor medio de la distribución F con 20 grados de libertad del numerador y 20 grados de libertad del denominador es menos que el valor medio de la distribución F con 5 grados de libertad del numerador y 5 grados de libertad del denominador.

Debido a que ambas poblaciones padres son normales y tienen la misma varianza, y las muestras y las poblaciones son independientes, ya lo sabes v₁ = n₁ - 1 grados de libertad del numerador =, y que v₂ = n₂ - 1 grados de libertad del denominador =.

Para calcular la varianza, se utiliza la siguiente fórmula:

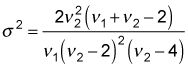
Tenga en cuenta que la fórmula de la varianza requiere que los grados de libertad del denominador sea mayor que 4 de lo contrario, la variación se vuelve negativa o indefinido.

La desviación estándar es la raíz cuadrada de la varianza:

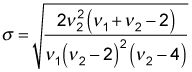
La varianza y la desviación estándar se utilizan como medidas de cómo extender los valores de la distribución F se comparan con el valor esperado.

Por ejemplo, para el F-distribución con 5 grados de libertad del numerador y 5 grados de libertad del denominador, la varianza es igual

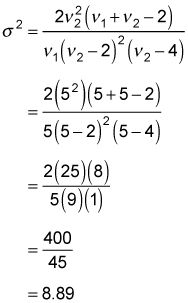
La desviación estándar es igual a la raíz cuadrada de 8,89 o 2,98.

Para la distribución F con 20 grados de libertad del numerador y 20 grados de libertad del denominador, la varianza es igual

La desviación estándar es igual a la raíz cuadrada de 0,29 o 0,54.

En la figura, el F-distribución con 20 grados de libertad del numerador y 20 grados de libertad del denominador tiene una cola que cae muy rápidamente (por lo que la distribución está menos extendido) en comparación con el F-distribución con 5 grados de libertad del numerador y 5 grados de libertad-denominador, por lo tanto, la distribución con 20 numerador y denominador grados de libertad tiene una menor varianza y la desviación estándar.